La Termodinamica dagli albori
fino alle soglie del XX secolo
Renato Lombardo
Dipartimento di Scienze e Tecnologie Biologiche,
Chimiche e Farmaceutiche dell’Università di Palermo
e-mail: renato.lombardo@unipa.it
Indice
3. Prima della Termodinamica 6
4. Le macchine a vapore e la nascita della Termodinamica
6. La Chimica e la Termodinamica
Abstract: Thermodynamics, the science of energy and entropy, is one of the most effective tools to understand how the Universe works. Born for utilitarian reasons, in the space of a few decades of the 19th century this discipline extended its field of application to increasingly vast and distant areas, causing an actual revolution in the way we look at Nature and we face the challenges of technology. Its development, although beginning many centuries ago, mainly characterized the 19th century. Its progress, initially slow and uneven, became increasingly rapid after the elucidation of the relationship between heat and temperature. The study of steam engines gave the first strong impetus, but it was with the overcoming of caloricist ideas that we arrived at the concepts of energy and entropy and the principles associated with them, thanks to the work of Kelvin and above all Clausius. Once these ideas were established, Gibbs and others developed applications in chemistry. At the end of the century, the application of statistics to the study of atomic-molecular systems led to the justification of the laws of thermodynamics and made it possible to redefine energy and entropy in microscopic terms.
Keywords: chimica fisica; storia della scienza; termodinamica; energia; entropia
Dal punto di vista del progresso della scienza, il XIX secolo fu un periodo di grande fermento. Nel volgere di pochi decenni, un numero tutto sommato esiguo di scienziati trasformò il mondo nel quale vivevano, facendolo diventare quello in cui viviamo noi oggi.
Lo sviluppo di una nuova disciplina, nata inizialmente per motivi squisitamente pratici, travolse visioni e consuetudini radicate trasformandosi ben presto in una vera e propria rivoluzione scientifica [1]. Questa disciplina era la Termodinamica.
Come sempre nella storia della scienza, lo sviluppo della Termodinamica fu possibile nel XIX secolo proprio perché fu in quel momento che si realizzarono le condizioni culturali, economiche e sociali adatte alla sua nascita. La separazione del concetto di calore da quello di temperatura, lo sviluppo del calcolo differenziale, le leggi dei gas sono solo alcune delle conquiste scientifiche che resero possibile questa rivoluzione. Così come Newton a suo tempo, anche gli scienziati del XIX secolo poterono “vedere più lontano” perché erano seduti sulle spalle dei “giganti” che li avevano preceduti, in particolare nel XVII e XVIII secolo.
Dal punto di vista sociale ed economico, è possibile ricordare fra le condizioni necessarie:
- lo sviluppo delle società scientifiche e la circolazione delle loro pubblicazioni, rese possibili da un sistema sempre più integrato di comunicazione e di trasporti in Europa e ben presto fra le due sponde dell’Atlantico;
- le guerre napoleoniche, con i cambiamenti sociali che ne seguirono, fra i quali una maggiore consapevolezza dell’importanza strategica della tecnologia, come quella mineraria e metallurgica;
- l’affermarsi delle istituzioni universitarie come sede centrale della ricerca scientifica oltre che dell’insegnamento.
La Termodinamica, a sua volta, ha stimolato e promosso enormi cambiamenti e innovazioni. Il motore a scoppio, la refrigerazione, i processi chimici industriali, solo per dirne alcuni, hanno avuto enorme impatto (nel bene e nel male) sulla società e sul nostro pianeta.
Essa è universale e i suoi principi si applicano a ogni cosa in Natura, dal motore di una automobile al più complesso degli esseri viventi e all’intero universo in espansione. Le leggi della Termodinamica costituiscono l’impalcatura sulla quale in maniera più o meno diretta si appoggiano tutte le altre discipline scientifiche. In chimica, in particolare, la Termodinamica riveste un ruolo cruciale per spiegare praticamente ogni fenomeno: la diffusione, la solubilità, l’equilibrio chimico, la cinetica chimica, il riconoscimento molecolare, il folding delle proteine e molto altro.
Il libro A history of thermodynamics [2], di Ingo Müller, ha come sottotitolo “la dottrina dell’energia e dell’entropia”. Esso racchiude perfettamente la centralità che questi due concetti hanno nella moderna visione della fisica e della chimica, insieme ai due principi della Termodinamica che vi sono associati.
Con la rivoluzione della Termodinamica l’energia si viene a trovare per la prima volta al centro delle interpretazioni dei fenomeni. Il suo ruolo è oggi irrinunciabile in quasi ogni modello o teoria, non solo nell’ambito strettamente fisico o chimico ma anche in ambiti molto distanti, dall’ecologia alla geologia, dall’economia alla scienza delle popolazioni. Analogamente, forse in modo più sottile e meno evidente, l’entropia, e il concetto di “spontaneità” intimamente connesso, hanno trovato un posto sempre più importante, non solo nella scienza.
2.1 L’approccio storico nella didattica della Termodinamica
La didattica della Termodinamica si deve confrontare con numerose sfide, dalla complessità e vastità delle sue implicazioni, alla difficoltà dell’astrazione matematica che richiede [3]. Forse anche per questo motivo ha spesso trascurato l’approccio storico, limitandosi al massimo a ricordare qualche nome o data e richiamare qualche aneddoto per cercare di stimolare l’interesse degli studenti.
Tuttavia, l’approccio storico-epistemologico all’insegnamento della scienza può offrire molto più di questo [4][5]. Introdurre aspetti storici promuove un maggiore approccio critico e permette di riconoscere più facilmente la scienza come un’impresa in continua evoluzione. La storia della scienza può contribuire a migliorare la comprensione degli studenti degli aspetti concettuali e del contesto sociale nel quale sono emerse alcune interpretazioni della Natura [6]. Essa può quindi contribuire ad una migliore comprensione del metodo scientifico, della natura della scienza e delle relazioni fra scienza, tecnologia e società, che oggi ancor di più che in passato è necessaria per lo sviluppo di competenze disciplinari e trasversali.
Questo è particolarmente vero nel caso dell’insegnamento della Termodinamica chimica che è risultato della fusione di due distinte discipline: la Chimica e la Termodinamica che, nonostante le loro somiglianze epistemologiche, seguono percorsi cognitivi diversi [7]. La sua storia è ricca di connessioni fra scienza, tecnologia e aspetti socioeconomici; nel suo linguaggio sono presenti residui di teorie passate e anche molte delle concezioni iniziali degli studenti sono simili alle idee e ai ragionamenti che sono stati affrontati e superati nel passato. Ecco, quindi, che la storia della scienza può essere un deposito di conoscenza da impiegare strategicamente per costruire, modificare e comunicare la rappresentazione della scienza e trasformare queste risorse in approcci didattici [6].
L’obiettivo di questo articolo è quello di tracciare in modo essenziale una descrizione della nascita e lo sviluppo delle principali teorie e modelli della Termodinamica. Naturalmente, essendo una disciplina così vasta, molto rimane comunque al di fuori di questa descrizione che è ben lontana dall’essere esaustiva.
Per una trattazione più ampia e approfondita si rimanda alla bibliografia e in particolare ad alcuni testi più generali. Oltre al già citato A history of thermodynamics [2], di Ingo Müller, si può fare riferimento a The World Of Physical Chemistry[8] di Keith J. Laidler. In aggiunta a questi due testi essenzialmente storici, Block by Block: The Historical and Theoretical Foundations of Thermodynamics [9] di Robert Hanlon riunisce l’approccio storico con quello di un manuale di base.
La Termodinamica è una disciplina ricca di equazioni e con una notazione alquanto specifica e complessa. I diversi autori di cui si tratterà nel prosieguo hanno impiegato notazioni e convenzioni spesso difformi fra loro. Per evitare di complicare ulteriormente la materia, si è deciso di impiegare il più possibile la nomenclatura, le convenzioni e la forma delle equazioni comunemente in uso nella moderna didattica della chimica, in particolare seguendo le scelte del manuale Chimica Fisica [10] di P. W. Atkins.
Tutte le citazioni riportate sono state tradotte dall’autore dall’originale o, in alcuni casi, dalla traduzione in inglese.
I fenomeni termici sono una parte importante del mondo che sperimentiamo ogni giorno. Il concetto di caldo (e freddo) ci accompagna fin dalla prima infanzia grazie al nostro sistema sensoriale che è in grado di trasmettere questa informazione al nostro cervello per mezzo di un insieme di recettori detti termocettori [11]. Alcuni di essi si attivano in un intervallo di temperatura compreso fra 15 °C e 45 °C, considerato dal nostro organismo “non pericoloso”, mentre altri si attivano a temperature più alte o più basse, segnalando anche il pericolo dell’esposizione a queste condizioni.
3.1 Gli antichi pensatori
L’osservazione dei fenomeni termici è certamente avvenuta fin dall’alba dell’umanità, dato il ruolo cruciale che il fuoco e le tecnologie a esso collegate ha avuto nello sviluppo delle comunità umane. Ciononostante, fino a tempi relativamente recenti, non si hanno testimonianze di un qualche tentativo sistematico per valutare quantitativamente quanto un corpo fosse caldo. Il concetto di temperatura sembra essere assente per buona parte della storia, pur se i fenomeni che avrebbero potuto essere alla base di questo concetto erano comunque ben noti agli antichi pensatori.
Probabilmente, uno dei motivi che ne hanno impedito uno sviluppo più precoce risiede nella visione di Aristotele (384-322 a.C.) che considerava caldo e freddo come due delle quattro qualità fondamentali della materia (insieme a secco e umido) che combinandosi fra loro costituivano i quattro elementi teorizzati inizialmente da Empedocle (515-430 ca. a.C.): fuoco, aria, acqua e terra.
Le idee di Aristotele, grazie anche agli scritti di Galeno di Pergamo (129-200 d.C.), ebbero grande influenza nel pensiero occidentale fino a tutto il medioevo. Secondo Aristotele, caldo e freddo erano qualità fondamentali, opposte fra loro, che non potevano quindi essere ridotte a termini relativi di unica proprietà (la temperatura) [12].
Seppur molto lentamente, però, l’idea di un qualche tipo di gradazione delle qualità di caldo e freddo cominciò a farsi spazio. Se già Galeno individuava quattro gradi di caldo e altrettanti di freddo, associati alla risposta fisiologica, più di mille anni dopo lo studioso Giovanni Marliani (1420-1483) [13][14]si spinse a proporre l’idea della “potenza del caldo” (e del freddo), distinta da quella dei quattro gradi di Galeno, che per un corpo dipendeva dal suo grado di calore, T, il suo volume, V, e la sua densità, D, secondo la relazione:
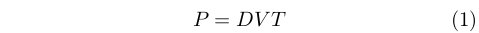 |
Una relazione che, seppur abbastanza casualmente, ne ricorda altre sviluppate molto più tardi.
3.2 La nascita della termometria
Alcuni autori dell’antichità come Filone di Bisanzio (III sec. a.C.) ed Erone di Alessandria (I sec. d.C.) avevano già costruito dei primi rudimentali dispositivi termoscopici, pur non cogliendo appieno l’idea di ciò che stavano misurando, ma limitandosi essenzialmente ad osservare gli effetti del riscaldamento sull’aria intrappolata al loro interno.
Fu solo nel corso del XVII sec. che la termometria poté cominciare a svilupparsi come risultato della fusione di due tendenze complementari: la prima fu quella verso l’astrazione, per la quale tutti gli aspetti qualitativi dei fenomeni venivano espunti dalla loro descrizione, lasciando soltanto entità descritte matematicamente e tralasciando, quindi, aspetti come la sensazione di caldo o freddo; la seconda fu quella verso lo sviluppo e l’impiego di strumenti di misura in grado di fornire un valore quantitativamente determinato da associare alla descrizione di un fenomeno [12].
Il termoscopio di Erone era noto in Sicilia fin dal XII sec. e nel corso del XVI sec. [15] e XVII sec. si erano diffuse in Europa varie ristampe sia in latino che in italiano dei suoi testi. A partire da queste conoscenze, diversi scienziati svilupparono degli strumenti più appropriati a misurare quanto un corpo fosse caldo.
Sebbene alcuni (fra cui lui stesso) abbiano attribuito l’invenzione del termometro a Galileo Galilei (1564-1642), è chiaro ormai che lui in effetti si limitò a perfezionare degli strumenti sviluppati precedentemente da altri studiosi. La prima attestazione scritta di un primitivo termometro[16] si deve, infatti, a Santorio Santori (1561-1636), mentre nello stesso periodo Robert Fludd (1574-1637) descriveva uno strumento simile nel suo trattato Meteorologica Cosmica [17]. Tutti questi termoscopi consistevano in un bulbo di vetro collegato a un tubo, che veniva immerso in un liquido (solitamente acqua) come illustrato in Figura 1. La variazione del volume dell’aria contenuta nel bulbo provocava una conseguente variazione dell’altezza del liquido nel tubo, fornendo una stima di quanto il corpo fosse “caldo”. Già nel trattato di Santorio si nota come fosse possibile una misura più precisa accostando una scala graduata al tubo.
Galileo fu uno dei primi ad affermare che “il freddo non è altro che l’assenza di caldo”, superando finalmente la dicotomia fra questi due concetti e riconducendoli entrambi alla stessa idea. La misura della temperatura con uno strumento permise anche di superare i limiti dei sensi umani, che potevano essere facilmente ingannati. Nel 1615, il diplomatico veneziano Gianfrancesco Sagredo (1571-1620), allievo di Galilei, scriveva al suo maestro [2]:
Con questi istrumenti ho chiaramente veduto, esser molto più freda l’aqua de’ nostri pozzi il verno che l’estate; e per me credo che l’istesso avenga delle fontane vive et luochi soteranei, anchorchè il senso nostro giudichi diversamente.
La misura dei termoscopi ad aria era, però, tutt’altro che precisa dato che il valore letto dipendeva dalla pressione atmosferica. Con la nascita dei termometri a liquido sigillati, che non risentivano della pressione esterna, la precisione e la facilità d’uso aumentarono notevolmente. Probabilmente si deve proprio a Galileo questo perfezionamento [18]e l’Accademia del Cimento fece largo uso di termometri ad alcool [19].
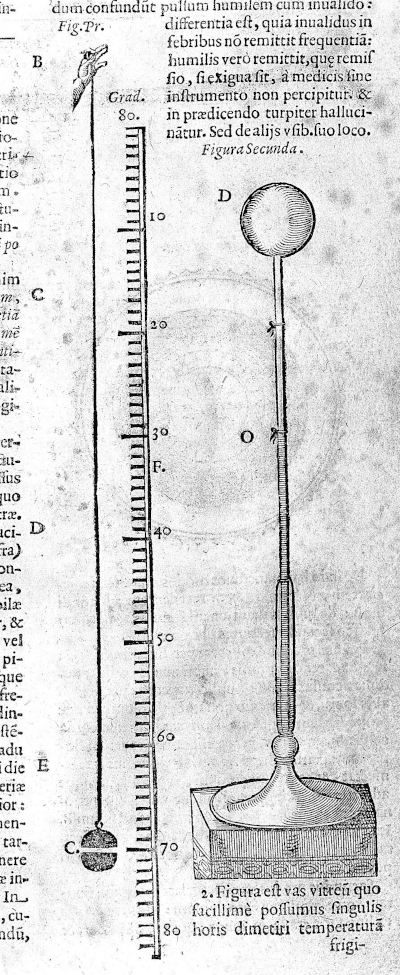 |
Figura 1. Descrizione del termoscopio di Santorio, dal suo trattato del 1626
Bisognerà aspettare il 1670 per vedere impiegato per la prima volta il termine temperatura da Robert Boyle (1627-1691) [20]. Nel XVIII sec. Daniel Gabriel Fahrenheit (1686-1734) mise a punto un termometro a liquido estremamente affidabile e soprattutto stabilì una scala standard di temperatura alla quale riferirsi mentre, nel 1742, Anders Celsius (1701-1744) propose la scala che da lui prende il nome [21].
3.3 Calore e temperatura
Lo sviluppo dei termometri permise finalmente di separare il concetto di temperatura da quello di calore che, per la gran parte della storia, erano stati spesso confusi. La definitiva distinzione si deve a Joseph Black (1728-1799) uno scienziato molto prolifico. Oltre ad aver identificato per primo l’anidride carbonica (che chiamò aria fissa), riuscì a dimostrare come fosse possibile determinare la quantità di calore a partire proprio da misure di temperatura, attraverso numerosi esperimenti che oggi diremmo di calorimetria.
Una volta compreso che il calore poteva essere ceduto o acquisito da un corpo e che questo trasferimento si poteva manifestare con una variazione di temperatura, Black poté sviluppare anche il concetto di calore specifico e quello di calore latente, cioè il calore “nascosto” che, pur essendo trasferito a un corpo durante una transizione da acqua a vapore o da ghiaccio ad acqua, non si manifestava con una variazione di temperatura.
Nonostante la sua fervente attività di ricerca, Black pubblicò molto poco e nulla a proposito delle sue ricerche sul calore. Per fortuna, un suo studente raccolse le sue lezioni in un libro che permise all’opera di Black di essere tramandata in modo sistematico [22].
La calorimetria ricevette un nuovo impulso (nonché il suo nome) grazie agli studi condotti in Francia da Antoine-Laurent de Lavoisier (1743-1794) e Pierre-Simon de Laplace (1749-1827). Il calorimetro a ghiaccio di loro invenzione permise misure molto precise che furono alla base della teoria del calore, esposta in Memoir sur la Chaleur [23]. Fu anche possibile osservare come il calore specifico dipendeva, oltre che dalla natura della sostanza considerata, anche dalla temperatura alla quale essa si trovava.
3.4 Le due teorie sul calore
Il concetto di calore, pur essendo stato descritto quantitativamente dagli esperimenti di calorimetria, rimaneva comunque piuttosto ambiguo per quel che riguardava la sua natura.
Le osservazioni fatte sui fenomeni termici condussero all’emergere di due teorie: per la teoria dinamica del calore esso andava ricondotto al movimento delle particelle dei corpi; per la teoria materiale del calore esso era una sostanza contenuta nei corpi [8] [24] [25].
L’effetto termico dello sfregamento era noto fin dall’antichità e già agli inizi del XVII sec. Francis Bacon (1561-1626) aveva proposto che il calore fosse correlato al movimento delle particelle costituenti la materia. Si parlava infatti di vis viva. Questa idea era condivisa da molti altri pensatori di quel periodo, fra i quali Isaac Newton (1643-1727) che nelle edizioni più tarde di Optiks [26] osservava come il calore fosse dovuto al rapido movimento delle particelle costituenti i corpi. La visione del calore come movimento conduceva naturalmente a una lettura in chiave cinetica di molti fenomeni. Newton propose, infatti, una teoria cinetica per l’evaporazione e per la dipendenza della pressione dei gas dalla temperatura. Anche Daniel Bernoulli (1700-1782) intorno al 1735 impiegò un ragionamento simile per dare conto della relazione di proporzionalità inversa fra volume e temperatura [25].
Lavoisier e Laplace furono, invece, fra i principali fautori della teoria materiale del calore. Essi consideravano il calore come un fluido indistruttibile, il calorico, che fluiva spontaneamente da un corpo più caldo a uno più freddo, senza mai scomparire, ma conservandosi inalterato nel corso di ogni trasformazione. La visione di Lavoisier era molto influenzata dal suo approccio chimico che considerava il calorico essenziale nello spiegare le reazioni di combustione. Esso era un costituente dell’ossigeno che veniva liberato durante la reazione manifestandosi come calore di combustione. Il calorico, infatti, poteva esistere in una forma libera, che dava origine alle variazioni di temperatura, o in una forma legata (il calore latente) che non manifestava effetti termici. L’idea del calore come una sostanza era in grado di spiegare molti fenomeni in modo coerente ed ebbe una vasta influenza sullo sviluppo della scienza per i successivi settanta anni.
Come detto, l’idea della natura materiale del calore condusse logicamente anche all’idea che esso si conservasse e che quindi fosse una funzione delle proprietà di un sistema. Era cioè quello che in termini moderni chiameremmo una funzione di stato. In particolare, si riteneva che dipendesse dalla pressione e dal volume di un corpo:
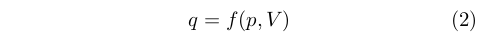 |
Nel 1815, per spiegare la velocità del suono nell’aria, Laplace espresse il calore come una funzione di pressione e volume di un gas in termini del rapporto fra le capacità termiche a volume e pressione costante γ= cv/cp:
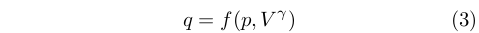 |
È bene notare, però, che per molti studiosi le due teorie non erano mutualmente esclusive. In memoir sur la Chaleur Lavoisier e Laplace cautamente affermavano [23][27]:
Noi non prenderemo una posizione definitiva fra le due ipotesi. Alcuni fenomeni sembrano favorire la prima, come il calore prodotto dallo sfregamento di due corpi solidi, per esempio; ma ne esistono altri che sono spiegati più semplicemente dalla seconda – forse sono entrambe vere contemporaneamente.
Anche Black, pur essendo essenzialmente un caloricista, non escludeva del tutto la visione meccanica del calore [22] [25].
4. Le macchine a vapore e la nascita della Termodinamica
Con lo sviluppo delle prime macchine a vapore, la relazione fra calore e lavoro divenne evidente. La spinta iniziale allo sviluppo di quella che oggi chiamiamo Termodinamica venne, infatti, dalla necessità di costruire macchine a vapore più efficienti, in particolare da impiegare per il funzionamento di pompe nell’industria mineraria, che nei secoli XVIII e XIX era in fortissima espansione e di importanza strategica per ogni nazione.
Sia la primissima macchina a vapore sviluppata da Thomas Savery (1650-1715) nel 1698 che la versione perfezionata da Thomas Newcomen (1664-1729) nel 1712, erano infatti piuttosto inefficienti e divoravano quantità enormi di combustibile.
4.1 La macchina di Watt
Fu solamente con l’intervento di James Watt (1736-1819) che dalle prime rudimentali macchine a vapore si passò a un tipo di macchina molto più efficiente e che rivestirà molta importanza nel successivo sviluppo della Termodinamica[28].
James Watt lavorava come tecnico all’università di Glasgow, dove era in contatto con Black. Riparando un modello didattico della macchina di Newcomen si rese conto di alcune possibili migliorie che lo portarono nel 1765 ad aggiungere un condensatore a temperatura significativamente più bassa rispetto alla caldaia già presente. Questo schema di macchina termica operante fra due temperature si rivelerà fondamentale per la successiva analisi teorica del funzionamento delle macchine a vapore.
Nel 1792 Davies Gilbert (1767-1839) osservò che il lavoro svolto durante un ciclo di funzionamento della macchina corrispondeva all’area sottesa alla curva p contro V. Nel 1796, insieme a un suo collaboratore, Watt sviluppo i diagrammi indicatori (detti anche diagrammi di Watt), che però vennero tenuti segreti fino al 1822 [29].
4.2 La macchina di Carnot
Si potrebbe scegliere l’anno 1824 come data di nascita della Termodinamica, sebbene questo termine in effetti fu coniato venticinque anni dopo, prima come aggettivo [30]e poi come sostantivo [31]. In quell’anno, infatti, veniva dato alle stampe Réflexions sur la puissance motrice du feu [32], un testo di sole 118 pagine scritto da un brillante studioso appena ventottenne, Sadi Carnot (1796-1832), figlio del famoso Lazare Carnot (1753-1823), scienziato, militare e politico, durante la Rivoluzione francese e l’impero napoleonico.1
Come il titolo fa immediatamente comprendere, in questo testo Carnot intendeva affrontare il problema della relazione fra calore e lavoro al fine di migliorare le macchine a vapore allora disponibili. Allo stesso tempo, però, egli iniziava la sua trattazione scrivendo [32]:
Tutti sanno che il calore può essere la causa del movimento […] ma il calore è anche responsabile dei vasti movimenti che avvengono sulla Terra.
È, quindi, evidente che fin dall’inizio l’interesse per la disciplina che sarà la Termodinamica andava ben oltre lo studio della macchina a vapore.
Per comprendere a pieno il funzionamento delle macchine termiche, Carnot sviluppò il concetto di macchina ideale (detta ora macchina di Carnot) alla quale poter ricondurre il funzionamento di tutte le macchine reali. La macchina ideale operava necessariamente fra le due temperature del serbatoio caldo (la caldaia), t2, e del serbatoio freddo (il condensatore), t1.
Carnot era un caloricista e affrontò, quindi, l’analisi del funzionamento delle macchine termiche in analogia a quello di un mulino ad acqua. In quest’ultimo l’acqua, cadendo dall’alto verso il basso, metteva in movimento una ruota e produceva lavoro, senza che vi fosse alcuna perdita di acqua. Allo stesso modo in una macchina termica il calorico fluiva dal serbatoio a temperatura più alta al serbatoio a temperatura più bassa, mettendo in movimento un pistone, senza che vi fosse alcuna perdita di calorico. Contrariamente alla visione moderna, quindi, Carnot riteneva che il lavoro non fosse svolto a scapito del calore trasferito.
Pur partendo da presupposti fisicamente errati, le principali conclusioni alle quali pervenne Carnot furono comunque coerenti e fisicamente sensate. Egli, infatti, realizzò che nessuna macchina termica (ideale o reale) poteva funzionare operando a un’unica temperatura, un’idea che noi ora interpretiamo alla luce del Secondo Principio della Termodinamica, ma che lui aveva dedotto dalla conservazione del calore [32]:
La produzione di potenza motrice nelle macchine a vapore non è dovuta al consumo del calore ma al suo trasporto da un corpo caldo a un corpo freddo […]. Da questo principio discende che, per ottenere una potenza motrice, non basta produrre calore: è anche necessario procurare del freddo; senza di esso il calore sarebbe inutile.
Carnot si rese conto che l’analisi del lavoro prodotto da una macchina termica non doveva focalizzarsi solo sul momento dell’espansione, durante la quale viene compiuto lavoro dalla macchina sull’ambiente, ma che si doveva tener conto anche della successiva fase di compressione, quando il lavoro viene compiuto dall’ambiente sulla macchina, per poter riportare il pistone indietro e permettere l’inizio di un altro ciclo di funzionamento.
Carnot suddivise la fase di espansione in uno stadio isotermo e un successivo stadio adiabatico (senza scambio di calore) e fece lo stesso per la fase di compressione, ottenendo il ben noto ciclo di Carnot a quattro stadi. Probabilmente la decisione di interporre due stadi adiabatici fra gli stati isotermi (nei quali il pistone era a contatto con uno dei due serbatoi) deriva dalle idee del padre Lazare, che nei suoi scritti di meccanica aveva sottolineato come per ottenere la massima efficienza bisognasse minimizzare ogni differenza nei punti di contatto fra le parti in movimento. Nella visione del figlio Sadi, questo si tradusse nell’evitare il contatto fra i due serbatoi a temperatura diversa, interponendo gli stadi adiabatici e permettendo al fluido nel cilindro di riscaldarsi o raffreddarsi in isolamento [25].
Anche il concetto di reversibilità, così importante in Termodinamica, fu introdotto da Carnot (pur non usando questo termine)2 sulla base di un’idea espressa da suo padre a proposito della geometria del movimento [33].
Carnot impiegò ingegnosamente l’idea dell’impossibilità del moto perpetuo per dimostrare che, a parità di combustibile consumato, si poteva ottenere il massimo lavoro da una macchina termica quando questa funzionava in modalità reversibile. Contrariamente alla trattazione moderna, però, egli non usò il concetto di efficienza (o rendimento), e. Nel senso moderno del termine essa corrisponde alla frazione di calore assorbito dal serbatoio caldo, Q2 che è stata convertita in lavoro, W, dalla macchina termica:
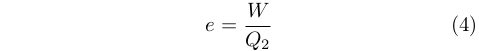 |
Questa idea, infatti, sarebbe stata in contrasto con la conservazione del calore.
Tuttavia, egli caratterizzò il comportamento della macchina termica in termini di quantità di potenza motrice prodotta durante il trasferimento di una specifica quantità di calorico. Poiché nella sua idea il calorico trasferito era pari a quello prelevato dal serbatoio caldo, Q2, la relazione alla quale pervenne è del tutto analoga a quella moderna:
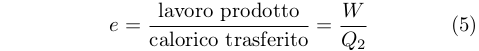 |
Un’ulteriore importante conclusione di Carnot fu che il lavoro prodotto da una macchina reversibile dipendeva esclusivamente dalle due temperature alle quali si trovava ad operare. Veniva così stabilito un limite massimo al lavoro che si poteva ottenere da qualsiasi macchina reale: indipendentemente dai dettagli tecnici e dai materiali impiegati non poteva essere superiore a quello di una corrispondente macchina ideale operante fra le stesse temperature.
Nella seconda parte del suo lavoro egli usò queste conclusioni per giustificare la maggiore efficienza delle macchine a vapore ad alta pressione rispetto a quelle a bassa pressione [32]:
È facile capire perché le macchine a vapore ad alta pressione sono migliori di quelle a bassa pressione; il loro vantaggio risiede essenzialmente nella loro capacità di sfruttare una maggiore caduta del calorico. Il vapore generato ad alta pressione si trova anche a una temperatura maggiore e poiché la temperatura del condensatore è più o meno sempre la stessa, la caduta di calorico è evidentemente maggiore.
Tuttavia, pur avendo in mente l’analogia del mulino ad acqua, Carnot intuì anche che non contava solamente la differenza di temperatura, ma anche che si otteneva un lavoro maggiore quando t1 era più bassa. Così, il lavoro prodotto in una macchina operante fra 100 °C e 90 °C era minore di quello che si poteva ottenere da una macchina operante fra 10 °C e 0 °C, pur se la differenza di temperatura era la stessa.
Egli non seppe stabilire con chiarezza quale fosse la dipendenza esatta, ma si limitò a esprimere l’efficienza (nel senso visto precedentemente) di una macchina termica ideale funzionante in un intervallo infinitesimo di temperatura, dt alla temperatura t come:
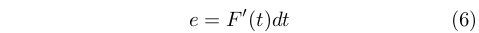 |
Dove F’(t) è una funziona universale della temperatura, che venne chiamata dagli studiosi successivi funzione d Carnot. Egli però non riuscì mai a determinare questa funzione.
Carnot morì prematuramente nel 1832, durante un’epidemia di colera. Sebbene molti attribuiscano a questo morbo la sua fine, secondo altri è possibile che fra le cause vi sia anche una malattia mentale, aggravatasi in coincidenza con l’epidemia [33]. Nel corso della sua vita pubblicò unicamente il libro del 1824; molti altri scritti, infatti, andarono perduti, perché i suoi beni vennero bruciati per evitare il contagio. Per fortuna, alcuni scritti affidati al fratello si salvarono e nel 1878 furono da lui donati alla Académie des Sciences.
Il libro di Carnot inizialmente non ebbe una grande influenza sulla comunità scientifica del tempo e ben presto divenne praticamente introvabile. Il suo lavoro, però, fu ripreso ed espanso da Émile Clapeyron (1799-1864), un compagno di studi di Carnot alla École Polytechnique.
Nel 1834 egli pubblicò Mémoire sur la puissance motrice de la chaleur [34], un lavoro che ebbe molta maggiore diffusione e che permise alle idee di Carnot di essere studiate (almeno indirettamente) da altri scienziati.
Il contributo di Clapeyron fu particolarmente importante perché riformulò il trattamento di Carnot nei termini molto più precisi del calcolo differenziale.
Egli fu anche il primo a illustrare i quattro stadi del ciclo di Carnot (Figura 2) in modo grafico in un diagramma sul piano p-V. Non è chiaro se questa sia stata una scoperta indipendente di Clapeyron o se, in qualche modo, fosse venuto a conoscenza dei diagrammi indicatori usati da Watt.
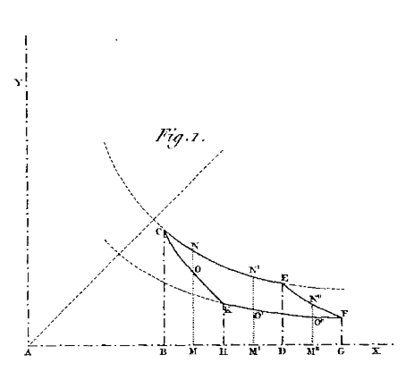 |
Figura 2. La prima rappresentazione grafica del ciclo di Carnot
4.3 La scala della temperatura assoluta
Fra gli studiosi che lessero avidamente il lavoro di Clapeyron ci fu senz’altro il giovane William Thomson (1824-1907), futuro lord Kelvin,3 che nel 1845 si recò a Parigi per lavorare con Henri-Victor Regnault (1810-1878). Nonostante le sue numerose ricerche, Kelvin non riuscì a trovare da nessuna parte il testo di Carnot, neppure alla biblioteca della École Polytechnique e poté soltanto leggere il lavoro di Clapeyron. Quando anni dopo riuscì a leggerne una copia, definì il libro di Carnot come “un regalo alla scienza di portata epocale”.
Il fatto che l’efficienza della macchina di Carnot fosse indipendente dal fluido impiegato, suggerì a Kelvin di impiegare questo concetto per stabilire una scala della temperatura assoluta [35]:
Esiste un qualche principio sul quale è possibile basare una scala termometrica assoluta? Mi sembra che la teoria di Carnot sulla potenza motrice del calore permetta di dare una risposta positiva a questa domanda.
Contrariamente a quanto viene solitamente detto, però, Kelvin non propose di costruire la scala assoluta sulla base del funzionamento di una macchina di Carnot. Si rendeva perfettamente conto che non sarebbe stato pratico. Quello che fece fu di dimostrare che il lavoro che si poteva ottenere da tale macchina era proporzionale alle temperature espresse in gradi Celsius se a queste si aggiungeva una costante [8].
Lo sviluppo della scala della temperatura assoluta fu, comunque, un processo non immediato, durante il quale Kelvin tornò più volte sui suoi passi. Inizialmente non colse neppure appieno il senso dell’analisi di Carnot, tanto da affermare nel 1848 che [35]:
Una unità di calore che si allontana da un corpo A ad una temperatura T° di questa scala verso un corpo B alla temperatura (T – 1)° avrebbe lo stesso effetto, qualunque sia il numero T. Questa potrebbe essere chiamata una scala assoluta.
Tale affermazione era ovviamente in contrasto con l’analisi originale di Carnot, la quale indicava che il lavoro doveva diminuire all’aumentare di T. L’errore fu probabilmente dovuto al fatto che Kelvin non aveva ancora potuto leggere il libro di Carnot, ma soltanto il lavoro di Clapeyron. Un anno dopo, però, riportava correttamente dei calcoli sul lavoro prodotto a diverse temperature che si trovavano in accordo con quanto affermato da Carnot [30].
In linea di principio, sarebbe stato possibile definire un numero arbitrario di scale della temperatura assoluta sulla base della macchina di Carnot. L’unico limite era che minore era la temperatura del serbatoio freddo, maggiore doveva essere l’efficienza. Kelvin propose inizialmente (1849) una scala che si basava su una funzione logaritmica [2] e solo successivamente (1851) si rese conto che fosse più conveniente una relazione additiva simile alla scala della temperatura basata sull’espansione di un gas [8].
Già Joseph-Louis Gay-Lussac (1778-1850) aveva dimostrato che a pressione costante il volume di un gas dipendeva dalla temperatura secondo la relazione:
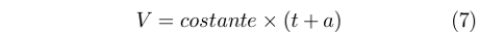 |
Dove t era la temperatura in Celsius e a era una costante. Questa scala aveva come limite il fatto di basarsi su una particolare sostanza. Il problema fu in qualche modo superato introducendo il gas perfetto e la sua ben nota equazione di stato.
Il concetto di gas perfetto, come limite al quale tendono i gas reali a mano a mano che diventano più rarefatti, si basava proprio sui lavori di Regnault, con il quale Kelvin aveva collaborato e che teneva in grande stima [21] [36].
L’approccio caloricista costituì un limite a un ulteriore sviluppo delle idee di Carnot e, finché non venne superato, non furono possibili ulteriori progressi.
Abbandonare il calorico significava rigettare la legge di dipendenza del calore da pressione e temperatura, espressa nella equazione (2). A questo proposito, il confronto fra quanto era riportato nelle bozze del lavoro di Carnot:
La legge fondamentale che ci proponiamo di confermare sembra essere stata definita oltre ogni dubbio.
con la versione che venne poi affidata alle stampe:
La legge fondamentale che ci proponiamo di confermare sembra necessitare di ulteriori verifiche per essere definita oltre ogni dubbio.
permette di capire come lo stesso Carnot avesse maturato dei dubbi sulla sua validità [24]. Prima della sua morte probabilmente Carnot era in procinto di abbandonare la sua visione caloricista, arrivando addirittura ad anticipare l’equivalenza fra lavoro e calore, come si può intuire dalla lettura dei suoi ultimi scritti, dove egli osservava che:
Ogni qual volta vi è una distruzione di potenza motrice vi è, allo stesso tempo, una produzione di calore in quantità esattamente proporzionale alla quantità di potenza motrice distrutta.
Anche Clapeyron, in qualche modo aveva intuito che calore e lavoro dovevano essere interconvertibili [34]:
Ne segue che una quantità di azione meccanica e una quantità di calore che passa da un corpo caldo a un corpo freddo sono quantità della stessa natura, e che è possibile scambiare l’una con l’altra; nella stessa maniera in cui in meccanica un corpo che viene lasciato cadere da una certa altezza e una massa in movimento con una certa velocità sono quantità dello stesso ordine, che possono essere trasformate l’una nell’altra con mezzi fisici.
Seppur egli stesse discutendo il funzionamento della macchina termica, più che la natura nel calore, le implicazioni delle sue affermazioni sono comunque importanti [24].
Il passaggio concettuale da un calorico indistruttibile a un calore che può convertirsi in lavoro (e viceversa) si dimostrerà assolutamente necessario per il seguente sviluppo della Termodinamica, ma arriverà solo lentamente.
5.1 L’equivalente meccanico del calore
Come è stato detto precedentemente, la teoria cinetica del calore aveva già numerosi fautori e, a partire dalla visione del calore come una forma di movimento, il passaggio a considerare che esso potesse convertirsi in lavoro era più che naturale. Di conseguenza, diversi autori ragionarono sull’equivalente meccanico del calore.
Fra i primi è possibile ricordare Benjamin Thompson (1753-1814) (futuro conte di Rumford), un americano naturalizzato inglese che, nel corso della sua vita picaresca, si ritrovò a lavorare in Baviera occupandosi di forniture militari. Egli intuì l’equivalenza fra calore e lavoro, osservando come le canne dei cannoni si riscaldassero enormemente durante il processo di lavorazione in cui veniva ricavata l’anima interna alla canna per trapanazione del bronzo (Figura 3) [37]:
[…] è inconcepibile pensare qualsiasi altra cosa che non che il calore non sia lo stesso di ciò che veniva fornito al metallo mentre il calore si manifestava in esso, vale a dire: movimento.
Dai suoi calcoli fu anche in grado di ricavare una prima stima dell’equivalente meccanico del calore, che tuttavia alla luce dei lavori successivi si rivelò piuttosto rozza.
Rumford, però, contribuì notevolmente allo sviluppo della scienza in modo più indiretto. Al suo ritorno in Inghilterra fondò la Royal Institution, che si potrebbe considerare come un precursore dei centri di ricerca moderni, nella quale chiamò a insegnare Thomas Young (1773-1829) e Humphry Davy (1778-1829), che daranno contributi fondamentali alla fisica e alla chimica.
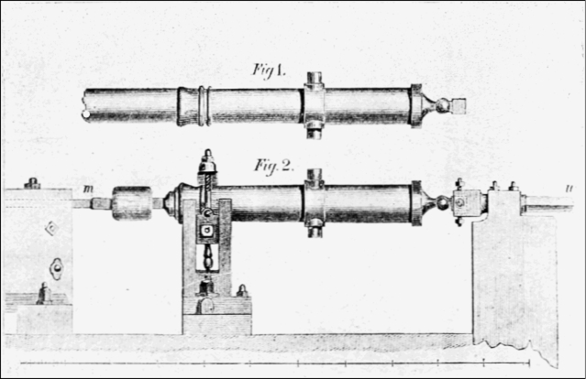 |
Figura 3. L’esperimento di Rumford
Le ricerche di Rumford non incisero molto sulle idee dei caloricisti per almeno altri quaranta anni. Un contributo alla discussione più articolato e convincente arrivò dal medico tedesco Julius Mayer (1814-1878) che, ragionando a partire dalla relazione fra cibo ingerito, calore prodotto e lavoro svolto, pervenne alla conclusione che calore e lavoro fossero interconvertibili in quanto erano due forme di ciò che lui chiamava forza (intendendolo però, in termini moderni di energia) che era indistruttibile.
Sebbene le conclusioni fossero essenzialmente corrette, i suoi ragionamenti erano spesso contorti, ricchi di termini metafisici e, a volte, accompagnati da errori che tradivano una certa ignoranza dei principi della meccanica. Per tali ragioni, il suo iniziale tentativo di pubblicare un lavoro su Annalen der Physik fu respinto. Solo dopo una profonda revisione esso fu pubblicato, nel 1842, sugli Annalen der Chemie und Physik [38]. Un’ulteriore debolezza del lavoro di Mayer è che egli non svolse direttamente alcun lavoro sperimentale, impiegando per i suoi calcoli i dati sui calori specifici ottenuti da Gay-Lussac.
Mayer era, comunque, arrivato a una stima ragionevole dell’equivalente meccanico del calore, a, pur non esplicitandone il valore nella sua pubblicazione. Egli calcolò, infatti, che per innalzare la temperatura di 1 kg di acqua di 1 °C era necessaria una caduta da 365 m di altezza. Da queste informazioni è possibile ricavare il valore (espresso in unità moderne) a = 3,57 J/cal, leggermente minore di quello oggi accettato di 4,18 J/cal. Solo nel 1845 Mayer pubblicò un lavoro nel quale riportava esplicitamente il valore di a e i calcoli con cui lo aveva ottenuto [25].
Il contributo di Mayer fu a lungo ignorato (se non ridicolizzato) dalla comunità scientifica del tempo, provocando in lui una forte depressione che lo portò a un tentativo di suicidio e a vari ricoveri in istituti per malattie mentali [8]. Con il tempo, però, il suo lavoro ottenne un riconoscimento maggiore tanto che, nel 1871, la Royal Society gli assegnò la Medaglia Copley, mentre la Académie des Science lo elesse come membro corrispondente.
Nonostante il contributo di Mayer, la determinazione dell’equivalenza fra calore e lavoro viene solitamente attribuita a James Prescott Joule (1818-1899). Questo figlio di un birraio di Manchester non ricevette alcuna formazione universitaria e fu educato a casa da insegnanti privati (fra i quali John Dalton!) [8].
L’interesse al problema della conversione fra calore e lavoro partiva dal suo interesse per gli esperimenti di Faraday e in particolare la generazione meccanica di elettricità. Egli osservò che il calore prodotto da un motore elettrico era pari a quello che si poteva ottenere se il lavoro impiegato per muovere il motore fosse stato invece utilizzato per produrre calore per attrito. Da questa e altre osservazioni arrivò a formulare la ben nota relazione fra potenza, P, intensità di corrente, i, e resistenza R che descrive l’effetto Joule [39] [40] e che permette quindi di stimare l’equivalenza con il calore dissipato in un tempo t:
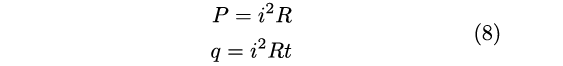 |
Joule si rese conto anche che la forza attrattiva di un elettromagnete era proporzionale a i2 e questa somiglianza lo condusse all’idea che vi fosse una connessione fra gli effetti meccanici e termici. Successivamente, esplorò altri tipi di legame fra l’azione meccanica e la temperatura dei corpi, tramite alcuni esperimenti sulla compressione dell’aria, osservando [41]:
Si è trovato che il calore liberato dalla compressione dell’aria è equivalente alla potenza meccanica impiegata e, vice versa, si è trovato che il calore assorbito nella rarefazione è equivalente alla potenza meccanica liberata.
Poco più avanti, Joule citava Mayer per aver proposto una equivalenza simile nel suo lavoro del 1842, “senza, tuttavia, aver tentato alcuna dimostrazione sperimentale della sua accuratezza”. Egli, al contrario, era un grande sperimentatore che procedeva sempre con estrema accuratezza, attenzione ai dettagli e inventiva.
Joule stimò l’equivalente meccanico del calore impiegando diversi approcci. Gli esperimenti elettrici fornirono un valore a = 4,60 J/cal, mentre dagli esperimenti sulla compressione dell’aria in diverse condizioni ottenne dei valori di a compresi fra 4,38 J/cal e 4,60 J/cal. Il fattore di conversione era, comunque, sempre all’interno di un intervallo del 15%, indipendentemente dal tipo di esperimento: riscaldamento per attrito, effetto Joule, compressione, ecc.
Questi risultati non potevano essere spiegati plausibilmente da alcuna teoria del calorico. L’unica spiegazione che ritenne accettabile fu che calore e lavoro fossero entrambi manifestazioni di una stessa grandezza fisica [42]. Nel 1847, il suo ben noto esperimento con la ruota a pale immersa in acqua (Figura 4) gli permise di determinare l’equivalente meccanico del calore con maggiore precisione.
Neppure le idee di Joule furono ben viste inizialmente dalla comunità scientifica. La mancanza di una formazione universitaria e di qualsiasi titolo o posizione accademica facevano di lui uno “scienziato dilettante”. Tutte le sue ricerche, infatti, erano state svolte in un laboratorio attrezzato e finanziato con rendite personali derivanti dalla fabbrica di birra della famiglia.
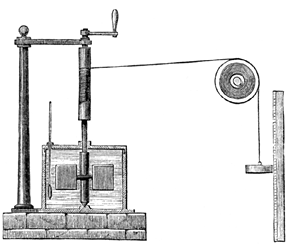 |
Figura 4. L’esperimento di Joule, come descritto su
Harper’s New Monthly Magazine, 231 del 1869
Nel 1847 Joule presentò parte dei suoi risultati ad una conferenza della British Association for the Advancement of Science, ad Oxford. In quella occasione ebbe modo di conoscere il futuro Lord Kelvin, da poco tornato dal lavoro a Parigi con Regnault. Kelvin fu molto colpito dal lavoro di Joule e i due ebbero diversi colloqui.
Kelvin e Joule si incontrarono nuovamente poche settimane dopo per una incredibile coincidenza: mentre Kelvin era in vacanza in Svizzera si imbatté per caso in Joule che cercava di misurare la differenza di temperatura fra la sommità e il fondo di una cascata. Joule si trovava in viaggio di nozze e la povera sposa attendeva pazientemente in carrozza che il marito terminasse le sue misurazioni.4
In questa sede vale la pena accennare all’accesa discussione sulla priorità della scoperta dell’equivalenza fra calore e lavoro che coinvolse Mayer e Joule nel 1848. Essa vide la comunità scientifica del tempo dividersi in due campi contrapposti che si scontrarono ripetutamente, anche in modo molto aspro: Mayer fu sostenuto fra gli altri da Helmholtz, Clausius e Tyndall, mentre Joule principalmente da scienziati britannici, Kelvin primo fra tutti. La data di pubblicazione del primo lavoro di Mayer è certamente precedente a quelli di Joule, ma le idee di Joule erano il frutto di un lavoro sperimentale e un’analisi ben più accurati e attenti. Come ebbe a dire C. Truesdell [43] a proposito del lavoro di Mayer del 1842:
Questo è il tipo di pubblicazione al quale nessuno scienziato guarderebbe neppure due volte, a meno che non sia in cerca di una ragione per negare la priorità a qualcun altro.
La questione è ormai poco importante. L’intuito di Mayer viene comunque riconosciuto da molti autori [2] [25]. Probabilmente se avesse operato in un minore isolamento scientifico e con una maggiore conoscenza matematica, la questione sarebbe stata risolta già da molto tempo.
5.2 Il primo principio
Kelvin aveva grande stima di Joule e del suo lavoro e i due collaborarono a lungo diventando anche buoni amici. Ciononostante, per un certo tempo Kelvin fu scettico rispetto alle sue idee. Nel 1849 pubblicò un resoconto delle teorie di Carnot [30] nel quale, pur citando più volte il lavoro di Joule, considerava comunque la conservazione del calore come base teorica “quasi universalmente accettata”.
Poco dopo, però, vi fu un repentino cambiamento di opinione. La lettura degli articoli di Joule e le conversazioni avute con lui portarono Kelvin a rifiutare le idee caloriciste, che fino ad allora aveva sostenuto, e ad accettare la teoria dinamica del calore.
Tuttavia, una cosa era accettare che calore e lavoro potessero trasformarsi l’uno nell’altro, ma ben altra cosa era l’idea che l’energia si conservasse. Questo passaggio richiese un’ulteriore elaborazione.
Sebbene l’energia sia oggi un concetto centrale a tutte le discipline scientifiche (e non solo), questo termine ha una storia tutto sommato recente. Esso fu introdotto per la prima volta nel 1807 da Thomas Young (1773-1829) e deve la sua origine al termine greco ἐνέργεια, che potremmo tradurre come azione efficace [44]. Young impiegò il termine nell’ambito della meccanica, ma fu solo verso fine del XIX secolo che esso fu universalmente accettato, anche in ambiti come la Termodinamica o l’Elettromagnetismo [2].
Indipendentemente dal termine impiegato, molti studiosi del passato, fra i quali Christiaan Huygens (1629-1695) e Gottfried von Leibniz (1646-1716), avevano dimostrato che l’energia si conservava in un sistema puramente meccanico, come nel caso delle collisioni fra sfere rigide. Il caso delle macchine termiche, però, era molto più complesso e poté essere affrontato solo dopo aver accettato la possibilità di conversione fra lavoro e calore.
Sia i lavori di Mayer che di Joule fornivano quantomeno un’indicazione che l’energia si conservasse ed entrambi lo ritenevano molto probabile. Mayer aveva riassunto questa idea nel motto latino: “Ex nihilo nil fit. Nil fit ad nihilum” [2].
Con il suo intuito aveva anche perfettamente compreso il funzionamento delle macchine termiche e lo aveva proposto ben prima dell’analisi che ne farà Clausius qualche anno più tardi, in modo molto più approfondito e circostanziato (cfr. infra):
[...] il calore assorbito dal vapore è sempre maggiore del calore rilasciato durante la condensazione. La loro differenza è il lavoro utile.
Nel 1846 William Grove (1811-1896) pubblicò On the Correlation of Physical Forces [45], nel quale enunciava chiaramente il principio di conservazione dell’energia. Un anno dopo, Hermann von Helmholtz (1821-1894) pubblicò Über die Erhaltung der Kraft [46], nel quale esponeva le sue idee sulla conservazione dell’energia in maniera molto dettagliata.5 Fra le altre cose dimostrò come l’energia, apparentemente andata perduta durante una collisione anelastica, era stata invece convertita in calore. Il lavoro di Helmholtz fu probabilmente quello che più di altri contribuì a far accettare la moderna visione di energia, calore e lavoro.6
Come spesso accade nella storia della scienza, l’idea della conservazione dell’energia era pronta a germogliare nella comunità scientifica del tempo; possiamo ritenere che, indifferentemente, sia Helmholtz che Joule o Mayer siamo stati i primi a proporla.7 Dei tre, però, Helmholtz fu sicuramente colui che ne diede una formulazione più chiara e circostanziata. Tuttavia, nonostante il suo intuito e la sua capacità matematica, Helmholtz non riuscì a esprimere il principio di conservazione dell’energia in forma matematica.
Questo ulteriore passo fu completato nel 1850 da Rudolf Clausius (1822-1888) in un ricco e dettagliato lavoro di analisi del funzionamento della macchina di Carnot [47], nel quale osservava saggiamente che la teoria dinamica del calore non invalidava gli aspetti principali del funzionamento della macchina di Carnot:
Una attenta analisi mostra che il nuovo metodo non contraddice il principio essenziale di Carnot, ma solo l’affermazione secondaria che non viene perso alcun calore, dato che può certamente essere che allo stesso tempo una certa quantità di calore sia consumata ed un’altra quantità sia trasferita dal corpo più caldo a quello più freddo, e che entrambe le quantità di calore siano in relazione.
È interessante notare come ancora nel 1850 Clausius condusse la sua analisi della macchina di Carnot senza aver mai avuto la possibilità di leggere il lavoro originale [47]:
Non sono stato in grado di ottenere una copia di questo libro e lo conosco solamente attraverso il lavoro di Clapeyron e Thomson [Kelvin].
Clausius abbandonò l’idea del calore come funzione di stato, che si conservava in un ciclo di funzionamento della macchina. Al suo posto, impiegò per la prima volta la funzione di stato U:
[U] ha le proprietà che sono comunemente assegnate al calore, essere una funzione di V e T ed essere quindi totalmente determinata dalle condizioni iniziali e finali del gas.
Clausius chiamò U il lavoro interno che definì come “la somma del calore libero e del calore consumato nel compiere lavoro interno”, intendendo la somma dell’energia cinetica e dell’energia potenziale dovuta alle forze intermolecolari. In termini moderni, essa è detta energia interna.
Grazie all’introduzione di U, Clausius fu in grado di formulare matematicamente il principio di conservazione dell’energia che in termini moderni esprimiamo con la ben nota relazione che lega la variazione di U al calore e lavoro scambiati dal sistema:8
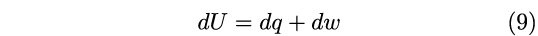 |
Con questa relazione, la conservazione dell’energia veniva definita per la prima volta in termini matematici, superando i limiti e le ambiguità delle espressioni verbali.
Sia Clapeyeron che Kelvin avevano riconosciuto l’importanza della funzione di Carnot riportata nella equazione (6) ma i loro sforzi di determinarla erano stati vani. Questa impresa venne invece portata a termine in pochi passaggi da Clausius che, come mostrato in dettaglio da Müller, fu il primo a sostenere in modo convincente che:
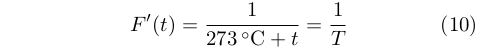 |
e quindi l’efficienza per una differenza di temperatura infinitesima era:
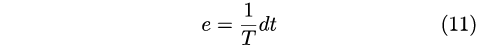 |
Clausius sviluppò una equazione per determinare l’efficienza di un ciclo di Carnot per un intervallo di temperatura arbitraria, ottenendo la nota relazione [48]:
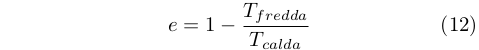 |
Nel 1851, avendo ormai abbandonato le idee caloriciste, Kelvin pubblicò un lungo lavoro che aveva per oggetto la teoria dinamica del calore [31] pubblicato inizialmente su Transactions of the Royal Society of Edinburgh, e l’anno seguente su The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science.
Nella sua analisi Kelvin citava con grande dettaglio il lavoro del suo amico Joule, unitamente ad alcuni esperimenti condotti da William Rankine (1820-1872) sull’espansione adiabatica del vapore, oltre a richiamare il lavoro di Clausius dell’anno precedente. Nel suo articolo, oltre ad associare espressamente U a una energia, Kelvin indicò per la prima volta la conservazione dell’energia come il primo principio della Termodinamica.
Anche Kelvin formulò la funzione di Carnot in termini analoghi all’equazione (10), ma affermò che questo risultato gli era stato suggerito da Joule in una lettera datata 9 dicembre 1848, pur riconoscendo che anche Clausius ne faceva uso. Questo problema di priorità sarà oggetto di uno scambio di lettere fra Kelvin e Clausius nel 1856 e una polemica molto aspra che ne seguì.
5.3 Il secondo principio
Uno dei motivi dei dubbi iniziali di Kelvin sulle idee di Joule risiedeva nel fatto che il lavoro sembrava poter essere convertito completamente in calore, senza alcun problema (come mostrato dagli esperimenti di Rumford e di Joule), ma vi erano dei limiti al processo contrario.
Questo aspetto rendeva più difficile accettare una qualche forma di loro equivalenza e, in ogni caso, complicava l’analisi del funzionamento delle macchine termiche. Sia Kelvin che Clausius si rendevano conto dell’importanza di questo problema e lo affrontarono, quasi contemporaneamente, a partire dalle pubblicazioni del 1850 (Clausius) [47] e 1851 (Kelvin) [31], che sono state introdotte precedentemente, alle quali ne seguirono altre negli anni successivi.
Nel 1850 Clausius formulò l’assioma che il calore non può passare da un corpo più freddo a un corpo più caldo che impiegò nella sua analisi del ciclo di Carnot. Questa affermazione fu criticata come troppo vaga e lo stesso Clausius non ne fu pienamente soddisfatto. Nel suo lavoro del 1851 Kelvin riprese questa idea e fornì una sua interpretazione che dimostrò essere equivalente a quella di Clausius:
È impossibile, per mezzo di un agente materiale inanimato, derivare un effetto meccanico da qualunque porzione di materia raffreddandola al di sotto della temperatura del più freddo degli oggetti circostanti.
Così come aveva riconosciuto la conservazione come il primo principio della Termodinamica, Kelvin allo stesso modo riconobbe in questa affermazione, o quella equivalente di Clausius, il secondo principio della Termodinamica.
Mentre il primo principio si limitava a stabilire una equivalenza, ad imporre un Universo nel quale ogni trasferimento di energia era perfettamente e simmetricamente bilanciato, il secondo principio rompeva invece tale simmetria. Fra tutte le possibili trasformazioni che rispettavano il primo principio, solo quelle che operavano in un verso erano compatibili anche con il secondo. Il dubbio di Kelvin sulla conversione di lavoro in calore e viceversa era così risolto.
È interessante notare come Kelvin nel suo enunciato del secondo principio si limiti a invocare questa limitazione solo per un agente materiale inanimato, lasciando quindi aperta la possibilità che gli esseri viventi potessero in qualche modo scavalcare il secondo principio e costituire quindi un caso eccezionale delle leggi della fisica. Questa possibilità verrà ben presto smentita [49].
Il sussistere dei due principi implicava quindi che il lavoro ottenibile in un ciclo di Carnot corrispondeva solamente a [31]:
[...] una frazione dell’equivalente meccanico del calore fornito; la parte rimanente è irrimediabilmente perduta per l’Umanità, e pertanto “dissipata”, seppur non annichilita.
L’energia si conservava, ma la sua capacità di compiere un lavoro veniva degradata.
L’idea della dissipazione dell’energia portò Kelvin a considerare che il mondo non poteva che esistere per un tempo finito, dato che l’energia andava continuamente degradandosi. La durata di questo tempo non era ancora misurabile ma non si adattava all’idea di tempi estremamente lunghi previsti da L’origine delle specie [50] di Charles Darwin (1809-1882). Kelvin vi si oppose strenuamente [51].
Negli anni successivi Kelvin si occupò sempre meno di Termodinamica. Era uno scienziato con molti interessi che contribuì significativamente anche ad altri campi della fisica. Al tempo stesso era anche interessato agli aspetti applicativi della scienza e, fra l’altro, ebbe un ruolo di primo piano nella posa del primo cavo telegrafico sottomarino fra le due sponde dell’Oceano Atlantico.
Clausius, invece continuò a occuparsi della Termodinamica per molto tempo. Partendo dalla sua formulazione del secondo principio nel 1854 fu in grado di dimostrare che l’efficienza di qualsiasi macchina reversibile operante fra due temperature era sempre la stessa [48].
Questo risultato era lo stesso ottenuto da Carnot, ma i presupposti sui quali si basava erano molto diversi. Mentre Carnot riteneva che il calore si conservasse, Clausius sapeva che il lavoro prodotto era la differenza fra il calore assorbito dal serbatoio caldo e quello ceduto al serbatoio freddo:
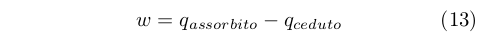 |
il che rendeva possibile esprimere l’efficienza come:
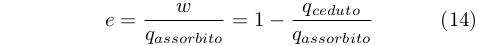 |
Dal confronto fra le equazioni (12) e (14) ricavò che:
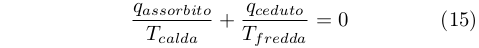 |
Clausius comprese che non era il calore a passare attraverso la macchina di Carnot, conservandosi, ma bensì un’altra grandezza, cioè q/T:
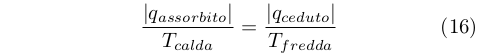 |
Questo risultato era già stato ottenuto da Kelvin nel 1851, senza che però egli gli attribuisse un particolare significato. Invece, uno dei più importanti risultati dell’analisi di Clausius del 1854 fu la possibilità di generalizzare l’equazione (15), estendendola a un qualunque percorso ciclico reversibile:
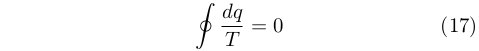 |
Questo passaggio fondamentale fu reso possibile dall’intuizione di Clausius che qualsiasi percorso sul piano p-V poteva essere decomposto in un numero arbitrario di cicli di Carnot di ampiezza infinitesimale. Il risultato rese chiaro che il rapporto q/T era una funzione di stato. Nel 1854 essa non aveva ancora un nome e Clausius la indicava con la lettera N.
La derivazione dell’equazione (17) a partire dal calcolo esplicito del lavoro nel ciclo di Carnot, che è il modo con la quale comunemente viene insegnata, arriverà solamente con il trattato di Termodinamica [25][52] scritto da Max Planck (1858-1947) nel 1897.
Clausius fu in grado di estendere il risultato dell’equazione (15) anche ai processi ciclici irreversibili ottenendo in questo caso che:
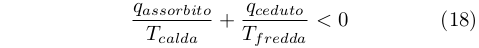 |
Successivamente, nel 1862, riunì le espressioni ottenute precedentemente tramite la disuguaglianza [53]:
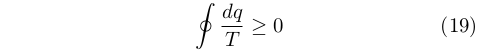 |
Fra la fine degli anni ’50 e l’inizio degli anni ’60 del XIX secolo Clausius si occupò della teoria cinetica dei gas (cfr. infra). In questo contesto introdusse il concetto di disgregazione [54], una misura della distanza fra le molecole di un corpo, che aveva le stesse unità di misura di q/T. Sebbene la disgregazione sia stata abbandonata, essa fu importante per dare vita alla grandezza entropia [55] che venne introdotta [56]da Clausius nel 1865:
[...] ritengo che sia meglio prendere nomi di grandezze così importanti per la scienza dalle lingue antiche, perché possono essere impiegati senza modifiche in tutte le lingue moderne. Propongo di chiamare la quantità S, in accordo con la parola greca ήτροπή, cioè il contenuto di trasformazione, l’entropia di un corpo. Ho scelto deliberatamente la parola entropia per essere la più simile possibile alla parola energia: le due grandezze a cui si riferiscono questi termini così sono strettamente legate per significato fisico che una certa somiglianza fra i loro nomi sembra essere appropriata.
Non è chiaro perché abbia scelto la lettera S ed è probabile che sia stata una scelta arbitraria. L’idea che derivi da Sadi, in onore di Carnot, come alcuni hanno detto, è ritenuta infondata da quasi tutti gli studiosi [2] [57].
L’entropia fu l’altra funzione di stato scoperta da Clausius, oltre a U, che si conservava nel ciclo di Carnot (e quindi in qualsiasi ciclo reversibile):
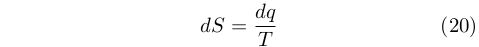 |
Fu così possibile riunire le equazioni (19) e (20) in un’unica equazione che oggi va sotto il nome di disuguaglianza di Clausius:
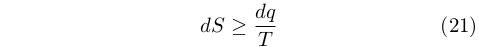 |
Per un processo finito fra A e B valeva quindi la relazione:
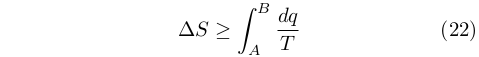 |
Questa equazione costituisce la formulazione matematica del secondo principio e completa la visione della Termodinamica, già in parte descritta dalla equazione (9).
Il lavoro del 1865 si chiudeva con due affermazioni perentorie che esprimevano i due principi in maniera efficace e concisa:
- l’energia dell’Universo è costante
- l’entropia dell’Universo tende verso un massimo
Qualche anno più tardi, Willard Gibbs (1839-1903) osservò che “la scienza della Termodinamica cominciò ad esistere” con l’articolo di Clausius del 1850. Poco più avanti, però riconosceva anche che [58]:
Nello sviluppo delle varie conseguenze delle proposizioni fondamentali della termodinamica, come applicazioni a tutti i tipi di fenomeni fisici, Clausius era affiancato, e forse superato, in attività e versatilità da Sir William Thomson [Kelvin].
Nel complesso, Kelvin fu spesso fra i primi a cogliere alcuni aspetti della Termodinamica, riconoscendone i principi e l’idea della dissipazione dell’energia. Tuttavia, probabilmente non si rese pienamente conto del cambiamento paradigmatico introdotto nella Termodinamica dal secondo principio.
Clausius, invece, colse pienamente questo aspetto. Buona parte della didattica della Termodinamica si basa sui lavori di Clausius a partire dal 1850. Non è un caso che Clausius fu uno dei primi ad aver lavorato sempre all’interno di una comunità universitaria. L’epoca degli scienziati/soldati/birrai come Rumford e Joule era ormai tramontata [2].
6. La Chimica e la Termodinamica
Intorno al 1870 i concetti fondanti della Termodinamica, riassunti concisamente nei due principi, erano ormai accettati e compresi dalla maggior parte della comunità scientifica. Fu allora che cominciarono i tentativi di impiegare la Termodinamica per l’interpretazione di fenomeni diversi dalle macchine termiche o dalla conversione di calore in lavoro.
La chimica si prestava molto bene all’applicazione di tali principi ad alcuni dei suoi problemi, in particolare, la spontaneità e la direzione delle reazioni chimiche per le quali, fino a quel momento, era stato impiegato con una certa ambiguità il concetto di affinità, riferendosi a volte alla possibilità di una reazione chimica di avvenire e altre, invece, alla velocità delle reazioni.
Lo sviluppo della Termodinamica chimica si deve a più autori che lavorarono in modo indipendente lungo direzioni abbastanza diverse l’uno dagli altri.
La visione più completa, coerente e rigorosa fu sviluppata da Gibbs negli anni fra il 1873 e il 1878. Nonostante ciò, il suo lavoro rimase per molto tempo quasi sconosciuto a causa della sua notazione piuttosto complessa, del suo stile di scrittura estremamente matematico e, non da ultimo, per aver pubblicato principalmente su giornali americani di bassa diffusione, per di più con titoli che erano poco chiari, se non addirittura fuorvianti [59][60]. Fu solo all’inizio del XX secolo che il suo contributo fu riconosciuto e la sua analisi rivaluta, approfondita e studiata.
Fino agli anni Venti del XX secolo furono principalmente la Termodinamica di Jacobus van ’t Hoff (1852-1911) e quella di Helmholtz a essere impiegate e studiate [8] nell’ambito chimico.
6.1 La Termodinamica di Gibbs
Gibbs fu assunto come professore di fisica teorica all’università di Yale nel 1871, quando ancora non aveva pubblicato alcun lavoro scientifico. Dopo essere stato uno dei primi a ricevere un Ph.D. negli Stati Uniti d’America nel 1863 (in ingegneria), aveva lavorato come tutor per l’università di Yale (dove il padre era stato professore di teologia) insegnando latino e matematica. Nel 1866 aveva trascorso un anno in Europa seguendo, a Parigi, Berlino e Heidelberg, i corsi insegnati da alcuni dei migliori scienziati del tempo, fra i quali Helmholtz. Tuttavia, nel corso del suo anno in Europa non aveva seguito nessun corso sulla Termodinamica e non si trova alcuna menzione di questa disciplina nei suoi appunti [59].
Ciononostante, poco dopo aver assunto l’incarico a Yale, Gibbs aveva cominciato a rivolgere il suo interesse verso la Termodinamica. Secondo un suo biografo (ed ex-studente) ciò era probabilmente dovuto a un breve interesse per le macchine a vapore nei primi anni, subito dopo il suo rientro negli Stati Uniti [59] Tuttavia, negli articoli di Gibbs, lo stile asciutto ed essenziale, estremamente matematico, non lasciava spazio alla descrizione delle ragioni che lo avevano spinto a intraprendere la sua ricerca.
L’approccio di Gibbs partiva da un’attenta analisi del lavoro di Clausius che, come è stato già detto, egli ammirava molto. Nei suoi articoli, invece, non veniva mai menzionato Kelvin. Il primo lavoro di Gibbs fu pubblicato nel 1873 su un oscuro giornale, Transactions of the Connecticut Academy, con un titolo che non lasciava intuire molto dell’importanza e profondità degli argomenti trattati: Metodi grafici nella termodinamica dei fluidi [61].
In esso proponeva l’impiego di un insieme più vasto di approcci grafici, rispetto ai già ben noti diagrammi di Watt; a suo parere essi erano “preferibili in molti casi per quanto riguardava chiarezza e convenienza”. Gibbs riteneva la geometria più efficace rispetto ai modelli meccanici, che egli reputava troppo poco aderenti alle equazioni [60].
In particolare, Gibbs espresse le proprietà di un fluido termodinamico tramite le corrispondenti caratteristiche delle curve che rappresentavano lo stato del fluido su un piano cartesiano, individuato dalle opportune variabili.
In un diagramma temperatura/entropia, ad esempio, era possibile rappresentare contemporaneamente il lavoro compiuto in un ciclo, il calore assorbito e il calore ceduto. Essi corrispondono, nella figura 5, rispettivamente all’area racchiusa dal ciclo, ABCD, all’area ABba e all’area CDdc.
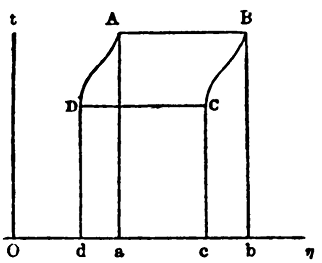 |
Figura 5. Un diagramma temperatura/entropia usato da Gibbs (η è il simbolo per l’entropia)
Si potrebbe essere portati a pensare che, nonostante l’utilità di questi metodi grafici, il lavoro di Gibbs offrisse tutto sommato un contributo trascurabile agli aspetti generali della Termodinamica. Invece, poche righe oltre la descrizione del suo approccio grafico, con il suo stile sobrio e asciutto, Gibbs si apprestava a cambiare radicalmente questa disciplina. In pochi passaggi egli pervenne a quella che chiamò l’equazione termodinamica fondamentale del fluido:
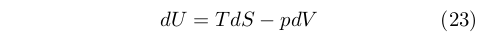 |
Con un approccio assolutamente innovativo, Gibbs eliminò il calore e il lavoro dalla sua visione e si concentrò, invece, sulle funzioni di stato. Prima di allora la Termodinamica aveva avuto come aspetto centrale le relazioni fra calore e lavoro. Dopo Gibbs, invece, “la Termodinamica diventò la teoria delle proprietà della materia all’equilibrio” [59].
Il secondo lavoro di Gibbs apparve sullo stesso giornale, pochi mesi dopo il primo. Ancora una volta il titolo non era particolarmente chiaro o invitante “Un metodo per la rappresentazione geometrica delle proprietà termodinamiche delle sostanze per mezzo di superfici” [61] e sembrava suggerire una semplice estensione dei metodi geometrici proposti precedentemente alle superfici tridimensionali.
In verità, in questo articolo Gibbs poneva maggior enfasi sul problema che intendeva affrontare: la caratterizzazione dello stato di equilibrio di un sistema, in qualsiasi stato fisico o combinazione di stati si trovasse.
A questo scopo, impiegò un unico approccio grafico: un diagramma tridimensionale nel quale gli assi erano: l’energia, l’entropia e il volume. A partire da questi, mise in relazione le proprietà delle superfici ottenute con le condizioni di equilibrio termodinamico, discutendo anche il punto critico che era stato descritto da Thomas Andrews (1813-1885) nel caso della CO2.
Gibbs dimostrò che affinché due fasi A e B siano in equilibrio non devono solamente avere la stessa pressione e temperatura, ma anche che le loro energie, entropie e volumi devono soddisfare la relazione:
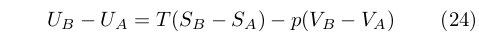 |
Da questa equazione scaturiva una relazione generale che Gibbs introdusse dicendo:
Se vogliamo esprimere in una singola equazione le condizioni necessarie e sufficienti per l’equilibrio termodinamico di una sostanza quando è circondata da un mezzo di pressione costante p e temperatura T, questa equazione può essere scritta come:
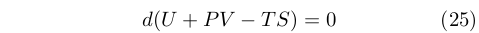 |
[...] La condizione di equilibrio stabile e quella per la quale il valore della grandezza fra parentesi è minimo.
La grandezza fra parentesi è quella che oggi viene chiamata energia di Gibbs [62]:
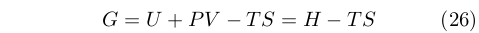 |
La quantità H = U + pV fu successivamente chiamata da Gibbs funzione calore a pressione costante, ma è ora nota con il nome entalpia, datole da Heike Kamerlingh Onnes (1853-1923) nel 1909 a partire dal greco ἐν θάλπω (calore interno) [63].
Gibbs poteva aspettarsi una seppur limitata circolazione dei suoi articoli grazie agli accordi di scambio di pubblicazioni che la Connecticut Academy of Arts and Sciences aveva con altre società in tutto il mondo. Tuttavia, egli si premurò di inviarne copia ad almeno 75 fra i più famosi scienziati del tempo.
Non molti però ebbero voglia o capacità di comprenderli. Kelvin scrisse a questo proposito: “Non trovo alcuna illuminazione sulla chimica o sulla termodinamica in Williard Gibbs” [8]. Sappiamo, però, che James Clerk Maxwell (1831-1879) lesse con attenzione questi due lavori e ne apprezzò appieno i risultati. Anche Maxwell, infatti, era un estimatore dell’approccio geometrico tanto che aggiunse un’estesa trattazione delle superfici di Gibbs nell’edizione del 1875 del suo trattato di Termodinamica [64]. L’idea delle superfici termodinamiche lo colpì talmente da ricostruirne una in gesso che mostrava le proprietà termodinamiche dell’acqua e che poi inviò a Gibbs in dono [65].
Con i suoi primi due lavori Gibbs aveva spiegato i criteri termodinamici alla base dell’equilibrio fra le fasi di un’unica sostanza e, partendo da questo, fu per lui naturale cercare di estendere l’idea anche ad altri equilibri.
Nel 1874 presentò alla ventina di membri della Connecticut Academy of Arts and Sciences un breve seminario sulle applicazioni della Termodinamica alla determinazione dell’equilibrio chimico. Da questo sviluppò un testo di oltre 300 pagine intitolato Sull’equilibrio delle sostanze eterogenee, che venne pubblicato in due parti: la prima [66] nel 1876 e la seconda [67] nel 1878. Sempre nel 1878 ne pubblicò anche un ampio riassunto [68] sull’American Journal of Science che aveva una circolazione molto più ampia.
In questo lungo trattato Gibbs ampliò il dominio della Termodinamica affrontando con un metodo unificato i fenomeni chimici, elastici, elettrochimici e di superficie. Per farlo introdusse fin dal principio il concetto di potenziale chimico, corrispondente ai coefficienti di ogni componente presente nell’equazione:
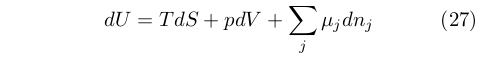 |
che può quindi essere definito come:
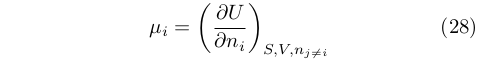 |
Poche righe dopo descriveva quella che oggi è nota con il nome di equazione fondamentale della Termodinamica chimica. Questa descrive la variazione dell’energia di Gibbs (che ovviamente lui non chiamava così e che indicava con ζ) al variare di pressione, temperatura o composizione:
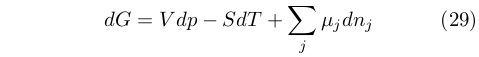 |
Il potenziale chimico può, pertanto, essere definito anche come derivata parziale di G, cosa che si fa comunemente nella didattica moderna:
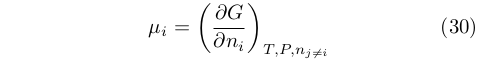 |
Questa variabile intensiva funzionava in maniera simile alle altre due proprietà intensive che caratterizzavano il sistema, T e p. La condizione di equilibrio in un sistema eterogeneo venne, quindi, espressa da Gibbs in analogia con la condizione di equilibrio meccanico e termico:
[nel caso dell’equilibrio meccanico e termico] la temperatura e la pressione devono essere costanti in tutta la massa [del sistema. Per l’equilibrio chimico] il potenziale di ogni sostanza componente deve essere costante nell’intera massa [del sistema].
La nozione di potenziale chimico permise a Gibbs di definire la regola delle fasi che troverà vastissima applicazione in molti problemi, ma sulla quale Gibbs non si soffermò molto.
Dopo aver pubblicato questi tre incredibili lavori, Gibbs non scrisse più molto di Termodinamica e si limitò per lo più a rielaborare i concetti espressi nel suo lungo trattato [69]. Rivolse, infatti, la sua attenzione verso altri argomenti della fisica, alcuni dei quali, però, avranno grande importanza nel successivo sviluppo della Termodinamica, come si vedrà più avanti.
6.2 Helmholtz e van’t Hoff
Mentre Gibbs sviluppava le sue idee sulla Termodinamica, alcuni altri scienziati, ignorando il suo lavoro, trovarono delle vie alternative per applicarla alla soluzione dei problemi chimici.
Dopo aver scritto il testo sulla conservazione dell’energia di cui si è già detto [46], Helmholtz si dedicò ad altri argomenti sia di fisica che di fisiologia. Egli era infatti anche un medico e fra i suoi contributi si ricorda, fra l’altro, l’invenzione dell’oftalmoscopio [70].
Verso gli anni ’80 del XIX secolo il suo interesse tornò alla Termodinamica e nel 1882 pubblicò un articolo nel quale affrontava il cambiamento chimico e la spontaneità delle reazioni dal punto di vista di questa disciplina [71].
Helmholtz cercò di risolvere il problema della spontaneità delle reazioni chimiche distinguendo fra una “energia libera”, che poteva essere convertita in altre forme e impiegata per fare lavoro, e una “energia legata”, che poteva essere rilasciata solamente sotto forma di calore. Basandosi anche lui sul lavoro di Clausius, espresse l’energia libera, A, come:
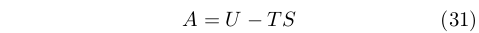 |
L’energia legata corrispondeva al prodotto TS.
Helmholtz dimostrò che, a volume e temperatura costanti, un processo è spontaneo nella direzione in cui l’energia libera diminuisce. Quella che lui chiamava energia libera viene oggi chiamata energia di Helmholtz [62]. A e G hanno entrambe il ruolo di fornire un criterio di spontaneità delle trasformazioni, però per condizioni diverse: A per volume e temperatura costanti, mentre G per pressione e temperatura costanti.
Se gli approcci e i risultati di Gibbs ed Helmholtz si somigliavano, la via scelta da van’t Hoff fu molto diversa. Il suo approccio era di tipo pratico, meno interessato al rigore teorico e più rivolto a trovare metodi direttamente applicabili in laboratorio.
Nel 1884 pubblicò Studi di dinamica chimica [72], che ebbe poi una seconda edizione nel 1896. Il titolo richiama, nell’uso del tempo, sia l’equilibrio chimico che la velocità delle reazioni e fu, in effetti, il primo libro a trattare entrambi gli argomenti [8].
Grazie anche a questo punto di vista, van’t Hoff fu fra i primi a riconoscere la natura dinamica dell’equilibrio chimico che, fra l’altro, era già stata proposta da William Williamson (1824-1904). Prima di questa idea, l’equilibrio chimico era sempre stato visto come un equilibrio di forze, in analogia a quello meccanico. Era così che lo descrivevano Cato Guldberg (1836-1902) e Peter Waage (1883-1900) quando, nel 1864, avevano introdotto l’idea della costante di equilibrio [73].
L’espressione della costante di equilibrio come la conosciamo oggi apparve in un articolo di Guldberg e Waage del 1879 e, seppur su basi più o meno empiriche, era comunemente accettata già prima dell’arrivo del libro di van’t Hoff. Egli, infatti, ne accettò la validità anche prima di dimostrarla per via teorica. Per riuscirci impiegò il concetto di lavoro di affinità chimica, wA, intendendo il lavoro che si poteva ottenere quando una reazione chimica avveniva in determinate condizioni. Sebbene oggi sappiamo che a temperatura e pressione costanti wA corrisponde alla variazione di energia di Gibbs, van’t Hoff non vi fece alcun riferimento.
Fu van’t Hoff a usare per primo il simbolo della doppia freccia (ma non con la notazione moderna delle frecce ad amo). Considerando una reazione arbitraria di equilibrio:
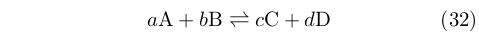 |
egli derivò che il lavoro wAA, compiuto quando la pressione di A veniva modificata da pA a pA,eq, era:
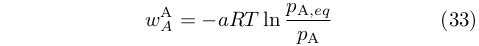 |
e ovviamente valevano analoghe equazioni anche per le altre specie coinvolte. Di conseguenza, il lavoro complessivo compiuto quando a moli di A e b moli di B venivano convertite in c moli di C e d moli di D era:
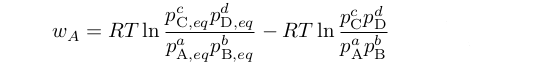 | (34) |
Essendo le pressioni di equilibrio valori determinati, l’argomento del primo logaritmo è una costante che era, per l’appunto, la costante di equilibrio
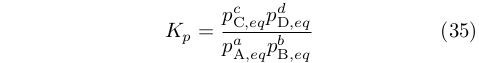 |
In termini moderni, tenendo conto della equivalenza fra ΔG e wA, è possibile riscrivere l’equazione (34) in funzione del rapporto di azione di massa Q/Kp:
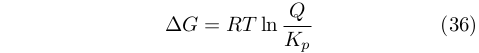 |
dove, , è detto quoziente di reazione.
Nello stesso trattato, van’t Hoff respinse le affermazioni fatte in precedenza da Julius Thomsen (1826-1909) e Marcellin Berthelot (1827-1907) che ritenevano che il calore ceduto durante una reazione fosse la ragione del suo procedere in una direzione. Egli si rese conto, invece, che il segno di q influenza solamente il cambiamento della costante di equilibrio, così come descritto dall’equazione che oggi porta il suo nome:
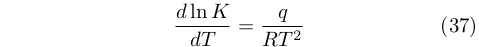 |
Questa relazione era stata comunque già proposta da August Friedrich Horstmann (1842-1929) nel 1868, e van’t Hoff lo riconobbe nel suo libro.
Pochi mesi dopo l’uscita del lavoro di van’t Hoff, il chimico francese Henri Louis Le Châtelier (1850-1936) riportò le conclusioni di van’t Hoff in un suo lavoro. Da allora vanno sotto il nome di principio di Le Châtelier. Essendo una persona molto mite e per nulla incline alle polemiche, van’t Hoff non cercò mai di correggere questo errore di attribuzione [8].
7. Gli atomi e la Termodinamica
Dopo i lavori di Clausius, di Gibbs e degli altri studiosi, era ormai chiaro che era possibile descrivere il comportamento dei sistemi termodinamici, la spontaneità dei processi e la condizione di equilibrio alla quale essi tendevano tramite poche variabili generali in relazione fra loro per mezzo di equazioni come la (21) o la (29).
I due principi della Termodinamica offrivano una descrizione netta e ineluttabile del funzionamento dell’Universo. In particolare, il secondo principio mostrava la profonda asimmetria dei fenomeni: esisteva una direzione ben precisa per il loro svolgersi. Al tempo stesso, però, i principi non fornivano vere e proprie spiegazioni. Non dicevano nulla su quale fosse in ultima analisi la ragione della loro validità universale.
Per alcuni, come Ernst Mach (1838-1916) e Pierre Duhem (1861-1916), questo non era un problema. Essi ritenevano che i principi della Termodinamica fossero leggi fenomenologiche autonome, che non necessitassero di ulteriori principi fisici sui quali basarsi.
Per molti altri, invece, il significato profondo dei principi risiedeva nella natura microscopica della materia: nell’energia cinetica e potenziale posseduta dagli atomi [74]. Bisognava, quindi, trovare un modo per conciliare la visione macroscopica, impiegata principalmente fino ad allora, con quella microscopica. La teoria dinamica del calore era già un buon punto di partenza. A partire da essa venne sviluppata la teoria cinetica dei gas e, successivamente, la visione più generale e completa che va sotto il nome di meccanica statistica [75].
7.1 La teoria cinetica dei gas
La teoria cinetica dei gas e la Termodinamica furono sviluppate negli stessi decenni, a volte dalle stesse persone. È quindi naturale che si riscontri una intima connessione fra queste due teorie.
Una volta definite le relazioni fra pressione, volume, temperatura e quantità di sostanza di un gas, fu possibile rivolgere l’attenzione a spiegare il comportamento dei gas nei termini del movimento delle loro molecole.
Anche prima che John Dalton (1766-1844) proponesse la sua teoria atomica, alcuni scienziati avevano cercato di spiegare la relazione pressione-volume in termini particellari. Già Newton aveva illustrato che un gas composto da atomi che si respingono con forza inversamente proporzionale al quadrato della distanza avrebbe mostrato, a sua volta, una pressione inversamente proporzionale al volume [76]. Fu, però, Bernoulli a proporre nel 1738 un modello dei gas simile a quello moderno (Figura 6) nel suo trattato Hydrodynamica [77].
Egli riteneva correttamente che la pressione fosse il risultato dei continui urti delle particelle di gas sulle pareti del contenitore e, ovviamente, condivideva l’idea che il calore non fosse altro che la manifestazione del movimento di queste particelle.
 |
Figura 6. Una rappresentazione schematica della
pressione dei gas, tratta da Hydrodynamica
Le sue idee arrivarono con grande anticipo rispetto ai tempi ed ebbero scarso effetto in una comunità scientifica nella quale la teoria del calorico era dominante [8]. Altri due precursori, John Herapath (1790-1868) e John James Waterson (1811-1883) ebbero altrettanta fortuna e rimasero per lo più ignorati.
L’interesse verso la possibilità di spiegare il comportamento dei gas tramite un approccio particellare fu ravvivato da un breve articolo [78] del 1856 scritto da Karl August Krönig (1822-1879). Il lavoro in sé non fu particolarmente importante, ma stimolò altri a intraprendere questa via.
Fra questi vi fu Clausius [79] [80] che nel 1857 derivò l’espressione che metteva in relazione le proprietà macroscopiche di un gas, come pressione e volume, con quelle microscopiche, come la massa delle particelle, m, e la loro velocità media, vmedia:
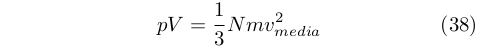 |
Dove N è il numero di particelle.
A partire da questa relazione, Clausius ricavò anche i valori della capacità termica molare a volume costante: CV,m=3/2 R e a pressione costante: Cp,m=5/2 R. Con questi risultati per la prima volta veniva creata una connessione fra la Termodinamica e la teoria cinetica dei gas.
Clausius aveva stimato delle velocità medie per alcuni gas, ma non aveva dei valori sperimentali a supporto di questi calcoli. I suoi risultati furono criticati aspramente da Christoph Buys-Ballot (1817-1890) che osservò con una certa malizia che le velocità previste erano talmente alte che l’odore della cena si sarebbe dovuto percepire nell’istante in cui si vedeva il maggiordomo entrare con il vassoio [2] [81].
Clausius rispose a questa critica nel 1858, affermando che le molecole non si muovevano in linea retta ma, urtando le une con le altre, cambiavano continuamente percorso. Questo lo portò a introdurre il concetto di cammino libero medio, λ, e metterlo in relazione con il raggio delle molecole, r, e la distanza media, d, alla quale si trovavano [82]:
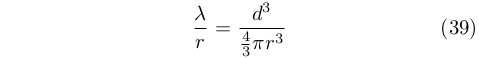 |
Questa equazione fu leggermente corretta da Maxwell; nel 1859 egli scrisse a George Stokes (1819-1903) descrivendo la teoria cinetica dei gas (Figura 7) che aveva sviluppato dopo aver letto l’articolo di Clausius. In soli quattro mesi era stato in grado di estendere e correggere i risultati arrivando a delle soluzioni originali che vennero pubblicate nel 1860, in due parti [83][84].
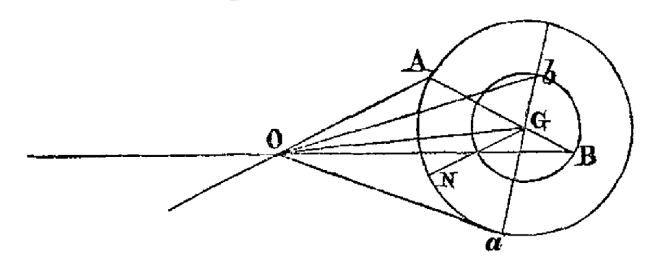 |
Figura 7. Uno schema tratto da Illustrations of the dynamical theory of gases di Maxwell
L’interesse di Clausius per la teoria cinetica dei gas risiedeva principalmente nel suo legame con la teoria dinamica del calore. Maxwell, invece, era più interessato a stimare il cammino libero medio (cosa che a Clausius non era riuscita) e le proprietà che si potevano derivare, come la viscosità, la conducibilità termica e la diffusione.
Per superare l’impossibilità di descrivere la posizione e la velocità di ogni particella, Maxwell decise di usare i metodi della statistica. Questa idea derivava direttamente da Clausius. Infatti, in una lettera scritta a Kelvin [2] riconosceva questo debito verso colui che, oltre ad aver introdotto il cammino libero medio, aveva proposto l’impiego di:
[…] metodi matematici […] per poter gestire statisticamente numeri immensi di molecole disponendole in gruppi secondo le loro direzioni, velocità, ecc.
Maxwell si rese conto anche di alcuni problemi nei risultati di Clausius e sostituì vmedia dell’equazione (38) con la radice della velocità quadratica media (vrms), cioè la radice della media della somma delle velocità quadratiche delle singole particelle:
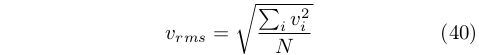 |
Quindi, ottenne:
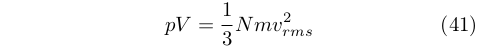 |
Proprio grazie all’introduzione dei metodi statistici, Maxwell fu un grado di dimostrare che i valori di velocità in una particolare direzione dello spazio obbedivano a una distribuzione normale:
Le velocità delle molecole spaziano fra tutti i valori, essendo distribuite in accordo con la stessa legge che prevale nella distribuzione degli errori di osservazione e in generale in tutti i casi in cui esiste una uniformità generale nella massa fra la apparente irregolarità in casi individuali.
7.2 Il secondo principio e la statistica
Una volta connessi i fenomeni macroscopici con quelli microscopici tramite un approccio statistico, Maxwell si rese conto che anche il secondo principio poggiava su queste basi. In una lettera inviata nel 1867 all’amico Peter Tait (1831-1901) immaginò il famoso esperimento mentale del demone, che poi riportò nel suo trattato Theory of Heat [64]:
Supponiamo che un recipiente sia diviso in due porzioni, A e B, da una parete nella quale vi è un piccolo foro e che un essere, che può vedere le singole molecole, apra e chiuda questo foro, in modo da permettere solo alle molecole più veloci il passaggio da A verso B, e solo a quelle più lente il passaggio da B verso A. Egli potrebbe, in questo modo, aumentare la temperatura di B ed abbassare quella di A, senza aver compiuto alcun lavoro, in contraddizione con il secondo principio della termodinamica.
Maxwell, si rendeva perfettamente conto di come questo esperimento mentale fosse impossibile nella pratica. Scriveva anche: “se potessimo far questo, potremmo violare il secondo principio. Solo che non siamo abbastanza capaci”.
È interessante notare che, con l’idea del demone onnisciente, capace di calcolare istantaneamente posizione e velocità di ogni particella, Maxwell anticipava di quasi un secolo il collegamento fra entropia e teoria dell’informazione [85].
In una lettera scritta a John William Strutt (1842-1919), futuro Lord Rayleigh, Maxwell chiarì in modo ancora più conciso ed efficace che la natura statistica del secondo principio non ne scalfiva assolutamente la validità, semmai il contrario:
Il secondo principio ha lo stesso grado di realtà dell’affermare che se gettiamo un bicchiere d’acqua nel mare, è impossibile tirare fuori nuovamente lo stesso bicchiere d’acqua.
Clausius non accettò mai l’interpretazione statistica di Maxwell e continuò a cercare, invece, un’interpretazione meccanica, a partire dal già citato concetto di disgregazione [53].
L’approccio meccanicistico fu perseguito inizialmente anche da Ludwig Boltzmann (1844-1906) che a soli 22 anni, prima ancora di conseguire il suo dottorato di ricerca, pubblicò un articolo [86] con il dichiarato obiettivo di fornire “una prova del secondo principio della Termodinamica puramente analitica e completamente generale e scoprire il teorema in meccanica che corrisponde ad esso”. Nonostante questo proposito, però i risultati furono poco soddisfacenti.
Nel suo articolo Boltzmann non menzionava il lavoro di Maxwell, probabilmente perché a quel tempo stava ancora imparando l’inglese. Due anni dopo, però, aveva letto con attenzione il suo lavoro sulla distribuzione delle velocità e sposò in pieno l’idea dell’approccio statistico al problema.
Fu così che estese il lavoro di Maxwell considerando anche delle particelle dotate di energia potenziale e deducendo una relazione che esprimeva la frazione di particelle dotate di energia εi, fi. In termini moderni questa relazione, in cui C è una costante, corrisponde alla distribuzione di Boltzmann:
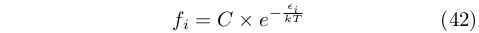 |
Il termine esponenziale è detto fattore di Boltzmann e si ritrova in varie forme in molte altre equazioni [87], mentre k è la ben nota costante di Boltzmann.
La costante C (o meglio, il suo inverso) venne ridefinita da Max Plank (1858-1947) che la chiamò somma sugli stati, ma che ora viene più comunemente detta funzione di partizione. Essa corrisponde alla somma di tutti i termini:
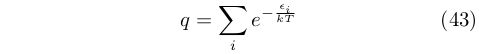 |
Per motivi essenzialmente di comodità di calcolo, nello sviluppo dell’equazione (42) Boltzmann considerò l’energia suddivisa in quantità discrete, ben prima che questa idea emergesse in fisica, e Plank fece uso di alcune delle procedure di Boltzmann nella sua trattazione della quantomeccanica [8].
Una volta stabilito come l’energia si distribuisse in un sistema di atomi e molecole, nel 1872 Boltzmann fu in grado ricavare il modo in cui un sistema raggiungeva l’equilibrio. Egli dimostrò che un aumento dell’entropia corrispondeva ad un aumento del “disordine” molecolare [88].
Per questa trattazione introdusse una funzione, H, che dipendeva dalla distribuzione delle velocità delle molecole di un gas, f:
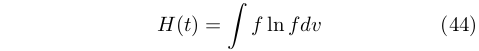 |
Boltzmann formulò un teorema che illustrava come H doveva inevitabilmente diminuire con il tempo, fino a raggiungere la distribuzione di Maxwell, nel qual caso rimaneva costante. La diminuzione di H corrispondeva all’aumento di S. Questo teorema è oggi noto come teorema H di Boltzmann [89]. Esso fu oggetto di alcune importanti critiche dalle quali Boltzmann dovette difendersi.
La prima fu mossa da Kelvin e riguardava il cosiddetto paradosso della reversibilità [90][91]. Kelvin affermava che sarebbe bastato invertire il movimento di ognuna delle particelle (le equazioni del moto sono reversibili), per osservare il sistema allontanarsi dall’equilibrio. Boltzmann rispose nel 1877 argomentando che in ogni sistema dinamico fra tutte le configurazioni possibili vi era un numero enorme di esse che corrispondevano a uno stato di equilibrio e solo una piccolissima frazione che invece conducevano lontano da esso. Egli ammetteva che fosse possibile trovare un particolare stato che portasse lontano dall’equilibrio (e quindi a un aumento di H e a una diminuzione di S), ma che questa possibilità era talmente piccola da non doverla considerare. Ancora una volta, la natura statistica del secondo principio mostrava la sua forza.
Una seconda critica fu mossa da Henri Poincaré (1854-1912) e riguardava il paradosso della ricorrenza. Secondo un suo teorema [92], ogni sistema dinamico doveva passare prima o poi per qualsiasi possibile configurazione. Poincaré riteneva, pertanto, che questo invalidasse il teorema. A questa critica si aggiunse anche Friedrich Zermelo (1871-1953) che fu particolarmente duro. Anche in questo caso, la spiegazione di Boltzmann seguiva la visione statistica: esistevano un numero molto più grande di configurazioni che corrispondevano a uno stato di equilibrio, sicuramente il sistema sarebbe potuto passare per un qualsiasi stato (anche di non equilibrio), ma ci sarebbe voluto un tempo così immenso da poter trascurare questa evenienza [93].
7.3 La meccanica statistica
La conoscenza della distribuzione delle particelle di un sistema aveva come scopo ultimo quello di poter determinare da essa le proprietà macroscopiche. Boltzmann affrontò questo aspetto in due lavori [94][95], pubblicati nel 1877 nei quali metteva in relazione l’entropia S con il numero W di configurazioni microscopiche corrispondenti a un determinato stato macroscopico, ricavando la celeberrima equazione (Figura 8) che si può considerare la nascita della meccanica statistica:
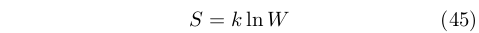 |
 |
Figura 8. La tomba di Boltzmann a Vienna riporta sulla lapide la sua famosa equazione9
Le configurazioni microscopiche sono dette anche microstati del sistema, mentre le configurazioni macroscopiche sono dette macrostati. W va anche sotto il nome di peso termodinamico di una configurazione.
L’entropia statistica proposta da Boltzmann fu esplorata anche da Gibbs, anche lui interessato alla meccanica statistica. Già nel 1876 osservava che [66]:
[…] l’impossibilità di una diminuzione non compensata dell’entropia sembra essersi ridotta a una improbabilità
Gibbs estese e raffinò ulteriormente le idee di Boltzmann, raccogliendo i suoi risultati nel libro Principi Elementari in Meccanica Statistica [96], pubblicato del 1902, poco prima della sua morte. L’interesse per la meccanica statistica era comunque legato anche ai suoi precedenti lavori di Termodinamica e il sottotitolo dell’opera recitava: “sviluppati con particolare riferimento ai fondamenti razionali della termodinamica”.
Gibbs ampliò la definizione di entropia statistica data da Boltzmann nell’equazione (45). Mentre Boltzmann trattava solo il caso in cui ogni possibile microstato aveva la stessa probabilità di manifestarsi degli altri, Gibbs considerò quello in cui per ogni microstato vi fosse una specifica probabilità pi di verificarsi. In questo caso l’espressione dell’entropia diventava:
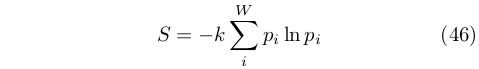 |
che si riduceva alla equazione (45) quando tutti gli stati avevano la stessa probabilità p = 1/W.
Mentre Maxwell e Boltzmann avevano applicato le loro considerazioni statistiche a un insieme di elementi identici, Gibbs propose un passo in avanti considerevole:
[…] per alcuni scopi, tuttavia, è desiderabile considerare una vista più ampia […] Possiamo immaginare un gran numero di sistemi della stessa natura, ma differenti per configurazioni e velocità che mostrano in un dato istante, e diversi non soltanto infinitesimamente, ma in un modo da poter comprendere ogni possibile combinazione di configurazioni e velocità.
Gibbs chiamò questo “gran numero di sistemi” un insieme statistico. Il vantaggio di impiegare questo approccio era che le energie degli atomi nel sistema potevano essere considerate variabili indipendenti. La collezione di tutti i sistemi venne chiamato da Gibbs un insieme canonico, mentre la collezione di insiemi caratterizzati tutti dalla stessa energia fu chiamato insieme microcanonico.
Boltzmann e Gibbs furono i principali artefici degli inizi della meccanica statistica e delle sue applicazioni alla Termodinamica. Tuttavia, bisogna anche ricordare che proprio nell’anno in cui Gibbs pubblicava il suo libro, il giovane Albert Einstein (1879-1955) pubblicava, appena ventiduenne [97], il suo terzo lavoro che trattava proprio le basi statistiche della Termodinamica, seguito da un secondo un anno dopo [98].
Sebbene il presente articolo si concluda a questo punto, la storia della Termodinamica non si è certamente fermata. Il suo sviluppo è continuato per tutto il XX secolo e non si è interrotto neppure nel XXI.
Nei primi anni del 1900 Walther Nerst (1864-1941) cominciò a lavorare su quello che sarebbe divenuto il teorema di Nernst [99][100] che espresse successivamente in termini di impossibilità di raggiungere lo zero assoluto. I successivi lavori di Franz Eugen Simon (1893-1956) portarono a una ulteriore revisione dell’idea di Nerst e alla formulazione di quello che sarà noto come il terzo principio della Termodinamica espresso nel 1930 come:
Allo zero assoluto le differenze di entropia fra tutti gli stati di un sistema che sono in equilibrio termodinamico interno, scompaiono.
Ben presto, l’idea di dover escludere gli esseri viventi dal campo di azione della Termodinamica, come aveva fatto Kelvin con la sua formulazione del secondo principio venne meno. Nel 1944 Erwin Schrödinger (1887-1961), fiducioso nella possibilità di comprendere gli esseri viventi con le leggi della fisica, pubblicò il suo celeberrimo libro dal titolo Cos’è la vita? [49]:
La materia vivente, pur non eludendo le “leggi della fisica” come stabilite fino a ora, probabilmente coinvolge “altre leggi della fisica” che comunque, una volta che verranno rivelate, formeranno una parte integrale della scienza così come le precedenti.
Nello stesso testo esprimeva le sue considerazioni sull’entropia e gli esseri viventi:
La cosa essenziale del metabolismo è che gli organismi riescono a liberarsi dell’entropia che non possono fare a meno di produrre essendo vivi.
I tempi erano ormai maturi per lo sviluppo da parte di Ilya Prigogine (1917-2003) della Termodinamica dei processi irreversibili [101] nel 1955. Il concetto di struttura dissipativa che ne derivava giustificò l’emergere di strutture ordinate dinamiche grazie al flusso di energia e materia fra esse e l’ambiente che le circonda. L’origine della vita venne così spiegata come un effetto delle leggi della Termodinamica.
Intanto, alla metà del XX secolo Claude Shannon (1916-2001) trovava un legame fra la teoria dell’informazione [85] che stava sviluppando e la formulazione statistica dell’entropia, con ricadute enormi nel campo della crittografia e della trasmissione e conservazione dei dati digitali.
In tempi più recenti, la Termodinamica quantistica ha cominciato a esplorare come i concetti della Termodinamica possano essere interpretati sulla scala quantomeccanica [102]. Un campo tutt’ora in gradissimo fermento e dove le sfide scientifiche e tecnologiche da affrontare sono enormi.
Indipendentemente dagli sviluppi che ci riserva il futuro, sembra comunque molto probabile che la Termodinamica, con i suoi principi, l’energia e l’entropia, continuerà a fornire una chiave di lettura irrinunciabile per molti fenomeni intorno a noi e dentro di noi.
Note
1 La famiglia Carnot ebbe un ruolo importante nella storia francese. Il fratello di Sadi, Lazare Hippolyte Carnot (1801-1888) fu ministro dell’istruzione, il figlio di quest’ultimo, Maries François Sadi Carnot (1837-1894) fu Presidente della Terza Repubblica Francese dal 1887 fino al 1894, quando fu assassinato a Lione dall’anarchico italiano Sante Caserio.
2Il termine verrà impiegato per la prima volta in senso termodinamico da Peter Tait solo nel 1876.
3 Per evitare confusione, nel prosieguo del testo William Thomson verrà sempre indicato come Kelvin, anche se il titolo di Barone Kelvin of Largs gli verrà conferito dalla regina Vittoria solo nel 1892. Il titolo prende il nome dal fiume Kelvin che passa attraverso l’università di Glasgow.
4 Questo aneddoto è riportato da vari autori, fra i quali Bent e Laidler. Tuttavia, sembra che non vi sia traccia scritta di questo avvenimento fino ad almeno 35 anni dopo la morte di Joule. Secondo alcuni autori, quindi, è possibile che la storia sia apocrifa. L’autore di questo articolo ha deciso comunque di crederci, sia perché esistono riferimenti a queste misure nei lavori di Joule sia per la bellezza di una simile coincidenza.
5 Sia Grove che Helmholtz usavano il termine forza per indicare l’energia.
6 Sebbene anche in testi moderni è molto comune parlare di calore e lavoro come forme di energia, è bene fare una importante distinzione: l’energia è una funzione di stato ed è, quindi, una proprietà di un sistema in determinate condizioni; calore e lavoro sono invece funzioni di percorso, sono proprietà di una trasformazione e ha senso definirli solo mentre sta avvenendo un processo. Per questo motivo, calore e lavoro sono modi per trasferire l’energia, più che forme di energia.
7 Secondo alcuni autori a questi potremmo aggiungere anche l’ingegnere danese Ludwig Colding (1815-1888) e il fisico tedesco Karl Holtzmann (1811-1865).
8 È bene notare che in questo testo si è deciso di adottare la notazione egoistica, nella quale il calore e il lavoro hanno segno positivo quando fanno aumentare l’energia interna del sistema. Proposta per la prima volta da Max Plank, la convenzione egoistica è quella adottata dalla IUPAC e dai moderni testi di Chimica Fisica.
9 La notazione usata nella lapide indica il logaritmo naturale come log, invece di ln, che è più comune oggi.