Principi elementari di reologia dei polimeri

La reologia dei polimeri si occupa sia della resistenza allo scorrimento del materiale polimerico allo stato liquido (soluzioni, stato sol, gel e fuso polimerico) sia della resistenza alla deformazione del materiale allo stato solido (polimero termoplastico, termoindurente, elastomero e composito a matrice polimerica e particelle eterogenee). Viscosità, elasticità e viscoelasticità sono le keyword fondamentali: in questo numero esaminiamo il comportamento non-Newtoniano dei fluidi polimerici.

Consideriamo un liquido tra due superfici piane e parallele, una fissa (quella inferiore, ad esempio) e l’altra mobile (quella superiore). Alla lastra superiore di area superficiale A applichiamo la forza di taglio T (parallela alla superficie) a cui corrisponde lo sforzo di taglio pari a:

$$\tau =\frac{T}{A}$$

Allora, lo strato liquido si deforma con un profilo di velocità u(y) (il diagramma triangolare di frecce in figura 1) dove dx è la deformazione applicata, du la velocità di deformazione e dy l’altezza dello strato fluido lungo l’asse y (trasversale alla direzione di deformazione x).

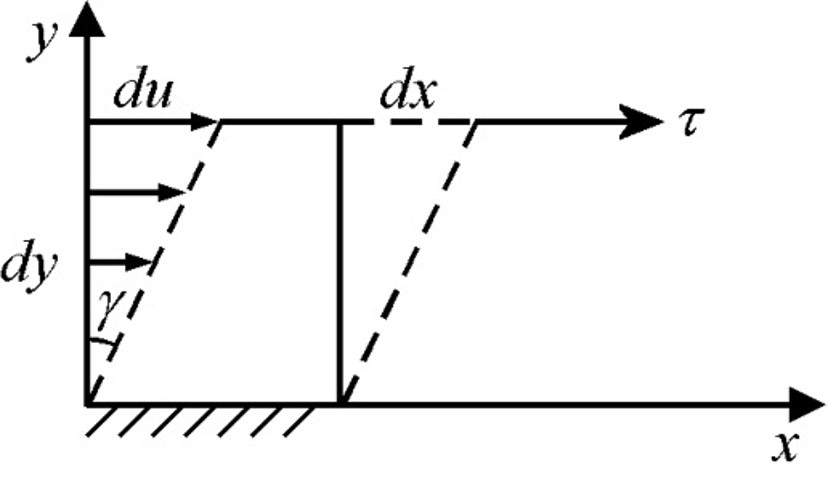Figura 1. Deformazione di taglio di un elemento di spessore dy

Otteniamo la deformazione angolare γ e la velocità di deformazione definita da:

$$\omega =\frac{d\gamma }{dt}$$

La velocità, u, varia lungo y secondo la funzione u = u(y) detta profilo di velocità. La velocità del fluido è solidale con i piatti: a contatto con il piatto superiore, la velocità di flusso coincide con la velocità di taglio applicata, diminuisce a mano a mano che si scende nello strato liquido, finché a contatto con il piatto inferiore il fluido risulta in quiete. Il profilo di velocità u(y) può essere una retta o una curva qualsiasi.

Il materiale sottoposto allo sforzo di taglio si deforma come un mazzo di carte: si conserva il volume, ma variano gli angoli degli spigoli laterali (Figura 2).

Figura 2. Deformazione di taglio di un mazzo di carte

Scriviamo ora l’equazione di Newton alla base dello scorrimento dei fluidi viscosi:

$$\tau =\eta \times \omega$$

dove τ è lo sforzo di taglio (shear-stress) applicato al liquido, ω la velocità di deformazione (shear-rate) e la costante di proporzionalità η è la viscosità del liquido espressa in Poise = [Pa × s].

La velocità di deformazione è la derivata temporale:

$$\frac{d\gamma }{dt}$$

Però, è altrettanto utile esprimerla come gradiente di velocità, dove u è il profilo di velocità lungo lo spessore y dello strato liquido:

$$\frac{du}{dy}$$

Risulta quindi:

$$\omega =\frac{d\gamma }{dt}=\frac{du}{dy}$$

In modo analogo, per i solidi elastici abbiamo l’equazione di Young:

$$\tau =G\times \gamma$$

dove lo sforzo di taglio è proporzionale alla deformazione γ mediante il modulo di taglio G: entrambe le equazioni descrivono la resistenza meccanica del materiale, allo stato liquido o solido, rispettivamente.

In reologia è necessario conoscere il gradiente di velocità ovvero:

$$\omega =\frac{du}{dy}$$

Allora, se il profilo di velocità è una retta, il gradiente è costante in tutto lo strato liquido, la relazione di Newton è valida e il fluido è detto Newtoniano; se il profilo di velocità è curvo (ad esempio, parabolico), il gradiente di velocità non è più costante, ma varierà da punto a punto nello spessore liquido, l’equazione di Newton sarà modificata e il fluido è detto non-Newtoniano.

In generale, la viscosità di un fluido è data dal rapporto shear-stress su shear-rate:

$$\eta =\frac{\tau }{\omega }$$

Per conoscere il comportamento reologico di un fluido è necessario costruire la curva di flusso τ = τ(ω) e la curva di viscosità η = η(ω) in cui lo sforzo o la viscosità è diagrammato in funzione della velocità di deformazione. Otteniamo allora un comportamento lineare (newtoniano) o non-lineare (non-newtoniano): se la curva è sovra-lineare il comportamento è detto shear-thickening e il fluido dilatante, se invece la curva è sub-lineare si parla di comportamento shear-thinning e di fluido pseudoplastico (Figura 3). In genere, il fuso polimerico ha una curva del tipo thinning che rappresenta la fingerprint della sua reologia.

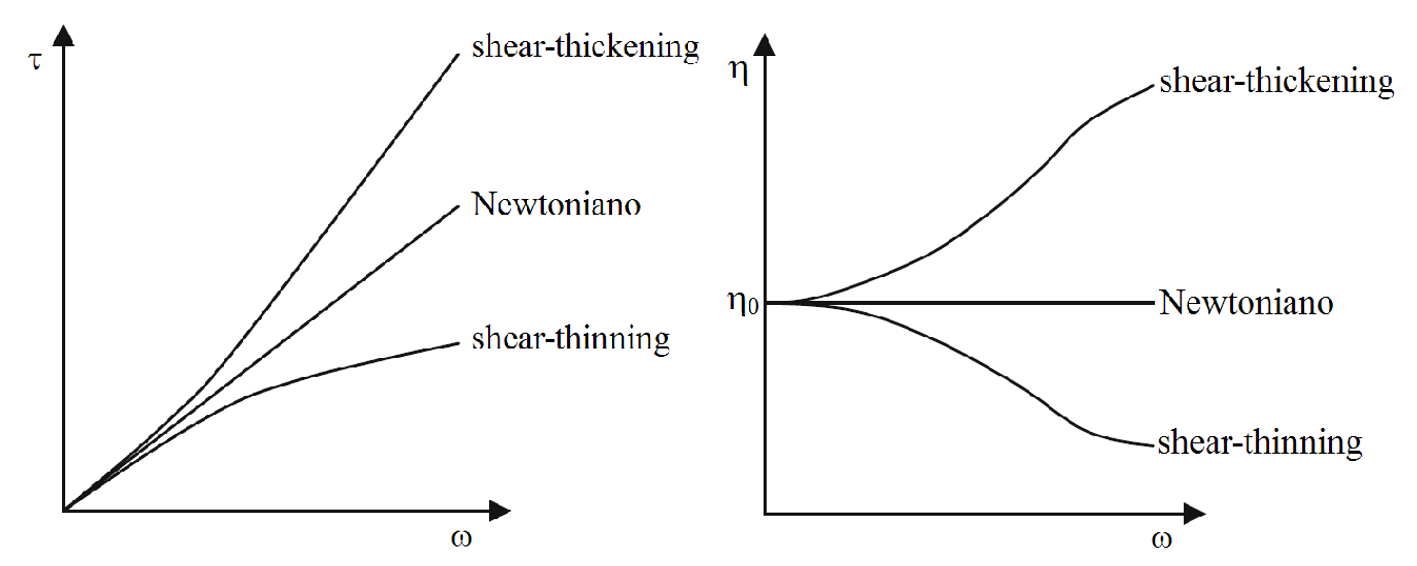Figura 3. Curve di flusso τ = τ(ω) (a destra) e curve di viscosità η = η(ω) (a sinistra) per liquidi Newtoniani o non-Newtoniani

A livello molecolare, questi comportamenti sono dovuti all’effetto del gradiente di velocità sulla macromolecola. La macromolecola in soluzione o nel fuso polimerico ha una forma sferoidale (detta random coil) sufficientemente grande (tipicamente, 100-200 nm, 1 nm= 10^-9 m, 1 miliardesimo di metro) da “sentire” il gradiente di velocità e, quindi, i segmenti di catena sperimentano differenti forze d’attrito viscoso. Dunque, le forze d’attrito danno luogo a un momento meccanico μ che fa ruotare lo sferoide attorno a un asse passante per il baricentro (Figura 4).

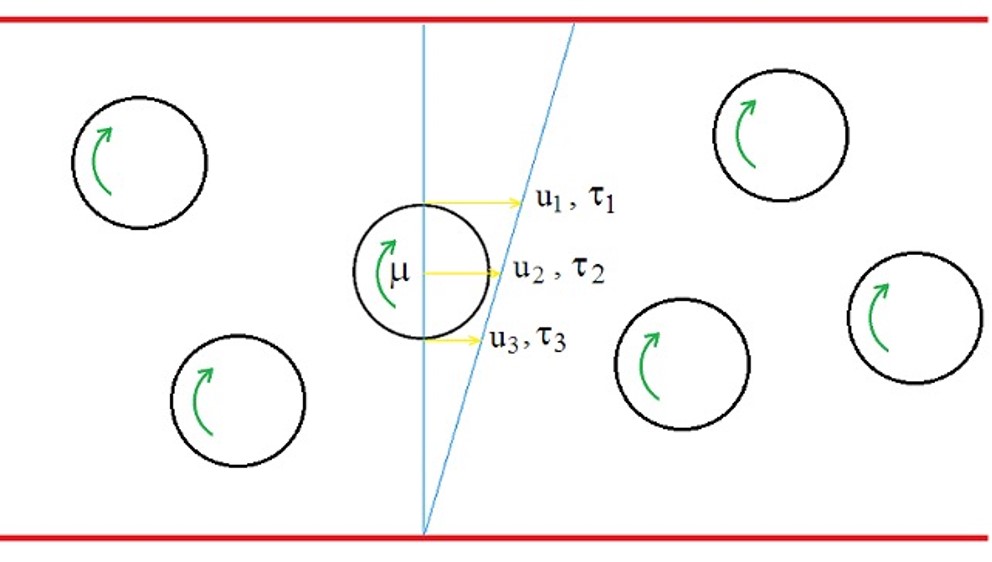Figura 4. Schema molecolare della rotazione delle macromolecole indotta dal gradiente di velocità

Allora, la macromolecola non solo trasla, trascinata dal flusso, ma anche ruota, dando luogo ad un moto roto-traslazionale. Essendo la viscosità una misura della resistenza del fluido a scorrere, se parte dell’energia del moto traslazionale viene dissipata in moto rotazionale, il flusso rallenta e la viscosità del fluido aumenta, ragion per cui, una soluzione polimerica risulta più viscosa del solvente puro.

All’aumentare della velocità di deformazione (e quindi del gradiente di velocità), gli sforzi di taglio tendono a schiacciare il random coil in un ellissoide orientato con la direzione del flusso. Di conseguenza, i moti rotazionali dissipativi si riducono e la viscosità del fluido diminuisce determinando il comportamento shear-thinning osservato per le soluzioni polimeriche e il fuso polimerico (Figura 5).

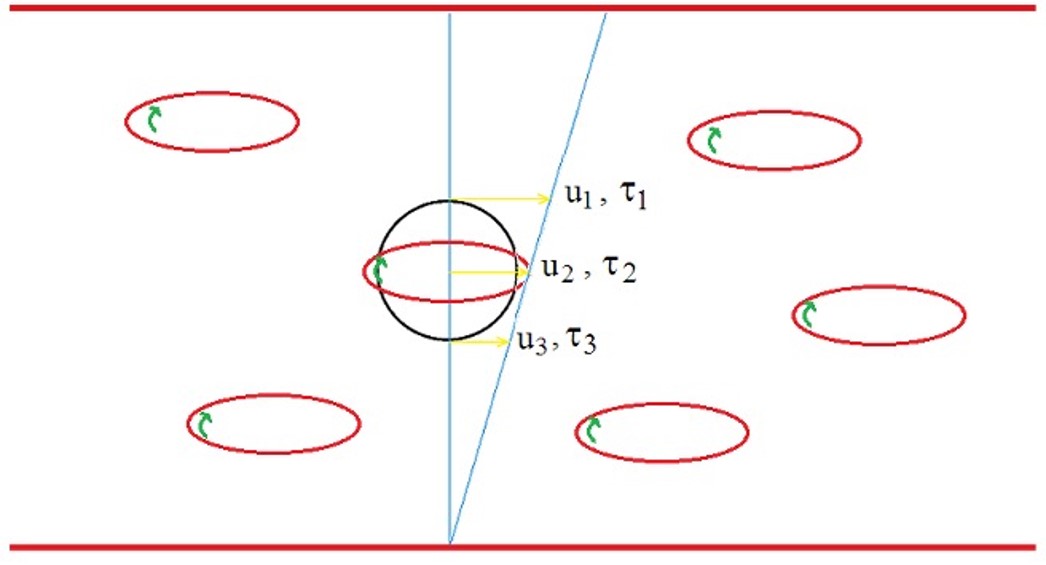Figura 5. Schema molecolare dell’orientamento degli ellissoidi col flusso

Al contrario, il comportamento shear-thickening è tipico delle dispersioni, ovvero di un liquido composito in cui sono disperse particelle eterogenee di dimensione micrometrica (1  μm= 10^–6 m), ciò è tipico dello stato sol in cui si formano aggregati micrometrici. Queste particelle si comportano in modo rigido, conservano la forma sferoidale con il flusso, ma all’aumentare della velocità di scorrimento si aggregano dando luogo a particelle più grandi che sperimentano un gradiente di velocità maggiore e, quindi, moti rotazionali dissipativi più intensi con il conseguente aumento della viscosità osservata (Figura 6).

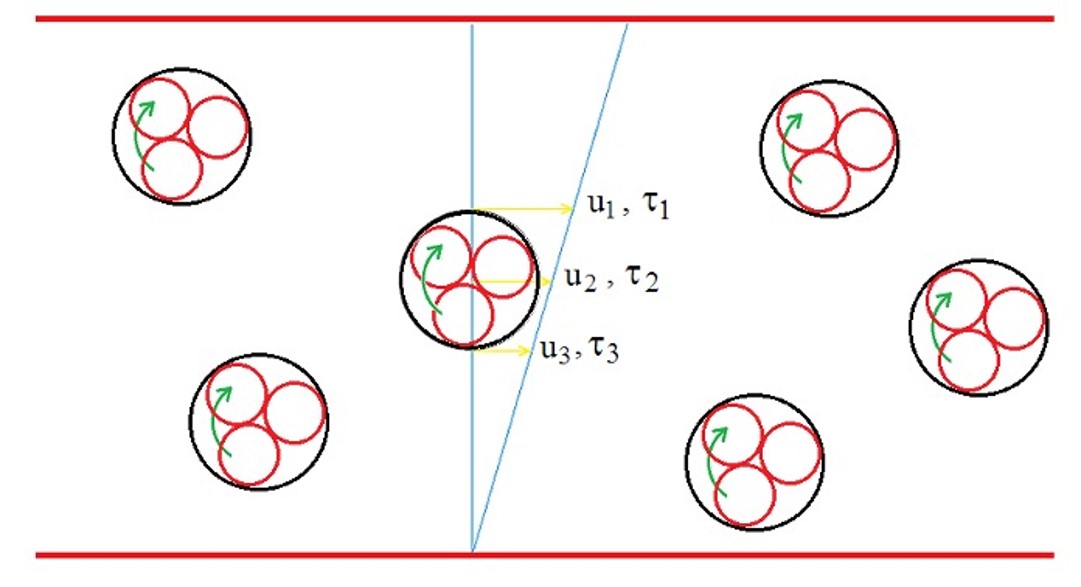Figura 6. Schema molecolare degli aggregati sol sotto l’azione del gradiente di velocità

Un fluido dilatante può essere descritto da un’equazione del tipo τ =  η₀ × ω² con andamento parabolico sovra-lineare, quindi:

$$\frac{\tau }{\omega }=\frac{{\eta }_0·{\omega }^2}{\omega }\Rightarrow \eta ={\eta }_0·\omega$$

da cui deriva un andamento lineare crescente della viscosità.

Analogamente, un fluido pseudoplastico può essere descritto da τ =  η₀ ×ω^1/2 con andamento sub-lineare, quindi:

$$\frac{\tau }{\omega }=\frac{{\eta }_0·{\omega }^{1/2}}{\omega }\Rightarrow \eta ={\eta }_0·{\omega }^{-1/2}$$

Da cui deriva un andamento decrescente della viscosità. In generale, le curve di flusso sono descritte da leggi di potenza, che rappresentano lo scostamento dalla linearità newtoniana.

Dalle curve di flusso e di viscosità risulta che il polymer melt, sia a basse che ad alte shear-rate, assume un comportamento Newtoniano, che può essere sfruttato utilmente nella caratterizzazione e nel processing dei polimeri, rispettivamente.

Il comportamento di molti fluidi non-Newtoniani, oltre ad essere funzione della velocità di taglio η = η(ω), è funzione del tempo η = η(t): in generale abbiamo η = η(ω,t). Mantenendo costante la velocità di deformazione ω = ω₀ (flusso stazionario), si costruisce la curva della viscosità dipendente dal tempo. Se il fluido ha un comportamento Newtoniano, allora osserviamo la retta costante η = η₀. Invece, se il fluido non-Newtoniano presenta una viscosità crescente nel tempo è detto reopettico; se mostra una viscosità decrescente nel tempo tixotropico (Figura 7).

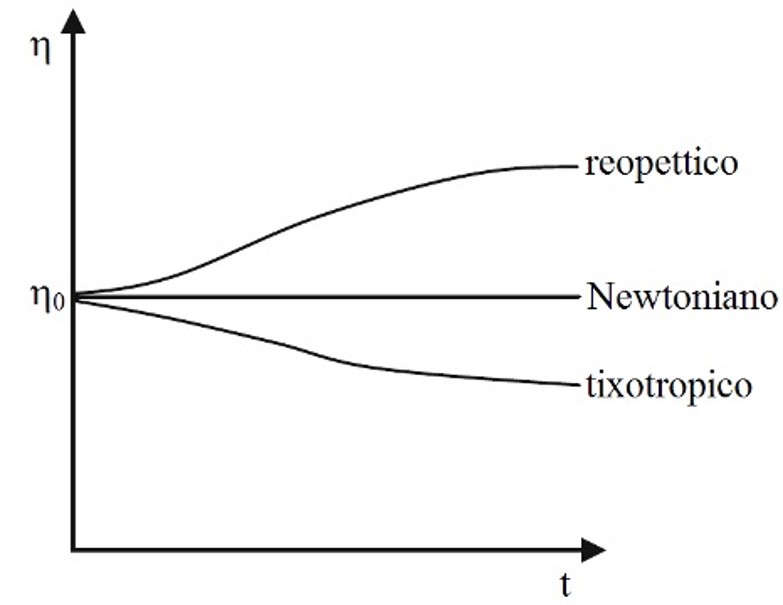Figura 7. Curve di viscosità in funzione del tempo η = η(t) per liquidi Newtoniani o non-Newtoniani

Un fluido tixotropico è caratterizzato da una struttura interna che rilassa lentamente, minimizzando la resistenza al flusso. È quanto accade nella transizione gel → sol in cui il reticolo tridimensionale (polymer network) dello stato gel, in virtù delle interazioni di non-legame di tipo van der Waals, si disgrega reversibilmente formando aggregati isolati, la dispersione propria dello stato sol. Possiamo dire che nello stato sol gli “aggregati macromolecolari sono dispersi nella matrice continua del solvente”, mentre nello stato gel “il solvente è disperso nella matrice continua macromolecolare” (Figura. 8).

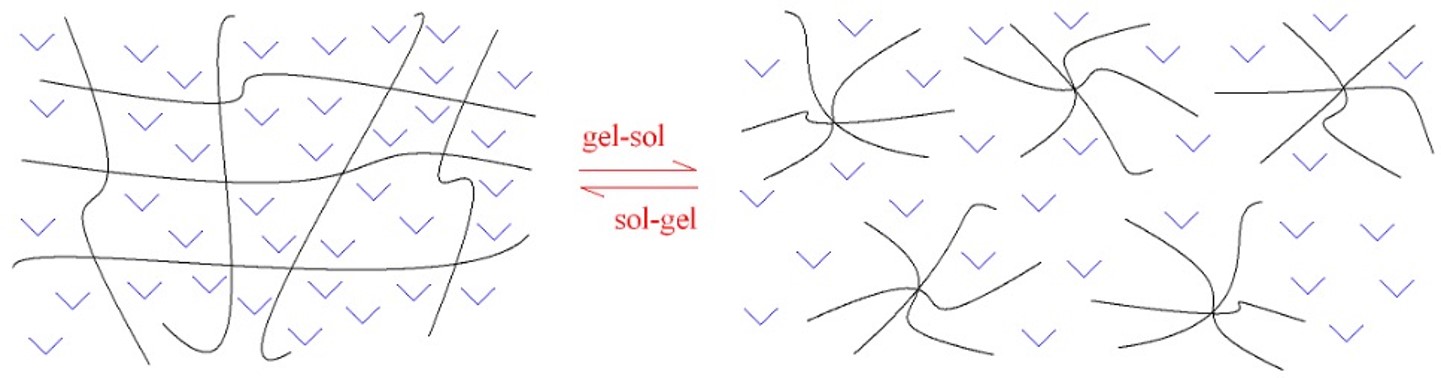Figura 8. Schema dell’equilibrio sol-gel