La prima congettura sul numero di atomi

La prima congettura sul numero degli atomi

Francesco Vissani

INFN, Laboratori Nazionali del Gran Sasso

Anche se a scuola si introduce sempre prima l’idea di atomo, bisogna ammettere che parlare di qualcosa di cui non si ha esperienza diretta può creare disagio agli studenti. Menzionare i filosofi antichi aiuta certo a rendere accettabile la discussione, ma non risolve il problema; presentare subito i risultati finiti della scienza, invece, non si può proprio fare. Come arrivarci più gradualmente? Una possibilità è quella di ripercorrere le principali tappe dell’esplorazione di questo concetto.

Ci concentriamo qui sul primo tentativo di determinare le dimensioni degli atomi, dovuto a un medico e filosofo del 1600, Magnenus. Nel suo libro Democrito redivivo: o degli atomi (1646) viene congetturato che il numero di atomi in una pallina di incenso sia circa 10 ¹⁸ - un miliardo di miliardi [1]. Vari scienziati e divulgatori ne fanno menzione [2 - 6], notando che questa stima non sia molto lontana da quelle più recenti. Curiosamente, però, non discutono (o a volte equivocano) l’argomentazione proposta, che non si basa su un modello di funzionamento dell’apparato olfattivo, ma piuttosto su una curiosa combinazione di spunti pliniani, democritei e archimedei.

Con queste motivazioni in mente, dopo aver discusso il contesto in cui questa congettura appare, esporremo il modo in cui Magnenus arrivò a formularla; subito dopo, confronteremo il valore che egli ottenne con altri più moderni e più credibili per passare, infine, alle conclusioni. Nel corso della discussione ci capiterà di toccare molti argomenti appartenenti a varie discipline, come filosofia, storia, chimica, fisiologia, astronomia e matematica; cercheremo di farlo nel modo più succinto possibile. Per una discussione più articolata, rimandiamo a un quaderno di appunti [7].

1. Magnenus ed il suo tempo

Jean Chrysostôme Magnen (1590 - 1679), il cui nome venne latinizzato in Magnenus, nacque in Borgogna a Luxeul (oggi Luxeuil-les-Bains) dove si laureò in Arti e Medicina nella vicina università di Dole. Fu un filosofo, chirurgo, medico teorico e farmacologo e divenne professore a Papiæ (oggi Pavia), anch’essa parte del Sacro Romano Impero e all’epoca sotto gli Asburgo, ramo spagnolo. Per maggiori notizie su di lui, si vedano [8, 9].

Il libro che ci interessa è in latino e nella versione scansionata è accessibile sulla rete internet. Ogni parte (preceduta da definizioni, principi e postulati) è divisa in capitoli, composti da un ben ordinato insieme di proposizioni e obiezioni. La forma della presentazione mima un po’ il modo di procedere di Euclide e non è in questo molto diversa, ad esempio, dal successivo The Sceptical Chymist: or Chymico-Physical Doubts & Paradoxes di Boyle (1661). L’argomento che ci interessa compare nella seconda parte, capitolo III, riguardante le proprietà degli atomi.

Il libro appartiene alla fase del dibattito filosofico in cui le reazioni all’aristotelismo iniziate già nel Rinascimento maturano i propri frutti. Vale la pena di consultare il testo di Melsen [10] per un quadro generale, ma raccomandiamo caldamente il saggio di Clericuzio [11], molto più focalizzato.

Due immediati predecessori di Magnenus, verso i quali egli riconosce un debito intellettuali, sono Daniel Sennert (1572 - 1637) e Sébastien Basson (1573 - 1640?); per gli scopi della presente discussione, è sufficiente ricordare i titoli di due loro opere (in latino): Sull’accordo e il disaccordo dei chimici con aristotelici e galenisti (1619) del primo e Filosofia naturale contro Aristotele, in dodici libri, in cui viene ripristinata la fisiologia segreta degli antichi e vengono confutati gli errori di Aristotele con solide ragioni (1649) del secondo. Altri filosofi ben noti e importanti per le sorti dell’atomismo, come Pierre Gassendi (1592 - 1655) o René Descartes (1596 - 1650), non esercitano alcuna significativa influenza sul pensiero di Magnenus e non figurano nel Democrito redivivo .

Peraltro, il contributo di Magnenus alla elaborazione delle dottrine filosofiche dell’atomismo non spicca per elementi qualitativamente nuovi [11], quanto piuttosto proprio per il tentativo cosciente di procedere verso un atomismo quantitativo. Cade a proposito un’annotazione del fisico e filosofo Lancelot Law Whyte [12]:

“L’effetto di questa tendenza relativa alle idee atomistiche è testimoniato dal fatto che tra il 1646 e il 1691 almeno sette scienziati europei (cinque prima di Newton) produssero o discussero stime, derivate da misure fisiche, di un limite superiore per le più piccole unità di materia utilizzate”

Naturalmente, il primo dei sette è proprio Magnenus, seguito da Charleton, Gassendi, Boyle, van Leeuwenhoek, Newton ed Halley.

Consideriamo l’effetto del Democrito redivivo oltremanica, da dove - come è ben noto - partiranno molti dei successivi impulsi che garantiranno il compimento della scienza moderna. Walter Charleton, un celebre collega di Magnenus, anch’egli medico e filosofo, tradurrà in inglese l’argomento quantitativo che ci interessa e lo presenterà nella sua nota opera sugli atomi [13] del 1654, aggiungendo considerazioni a supporto e dando beninteso credito al suo autore, come possiamo constatare dalla foto dell’estratto mostrata in figura 1.

Vissani.pdf

Figura 1 . Porzione iniziale della congettura di Magnenus secondo la descrizione di Charleton [13]; si noti, nella prima riga, l’esplicita attribuzione al suo autore; i numeri sono identici a quelli esibiti da Magnenus [1]

Anche Robert Boyle, spesso indicato come l’autore del primo libro di chimica in senso moderno e considerato come il primo a intraprendere la via della scienza (o l’ultimo a filosofare) tra i pensatori del 1600 inclinati verso l’atomismo, conosce e apprezza il contributo di Magnenus. Questo risulta evidente nell’introduzione di un suo breve saggio, riproposto all’attenzione generale negli anni ’50 del secolo scorso [14] e intitolato Of ye Atomicall Philosophy , dove egli espone alcune considerazioni:

“La Filosofia Atomica inventata o portata a richiesta da Democrito, Leucippo, Epicuro e loro contemporanei, [...] tanto opportunamente rianimata e abilmente celebrata in diverse parti d’Europa dalle dotte penne di Gassendi, Magnenus, Cartesio e loro discepoli come il nostro meritatamente famoso connazionale Sir Kenelm Digby e molti altri scrittori (specie quelli che trattano operazioni magnetiche ed elettriche) che oggi è cresciuta troppo da poter essere ancora derisa ed è sufficientemente considerabile da meritare un’indagine seria.”

Come è ben noto, Charleton e Boyle furono due dei primi membri della Royal Society. Concludiamo con alcune annotazioni sul principale spunto che consente a Magnenus di elaborare la propria congettura quantitativa sugli atomi. Si tratta de L’Arenario di Archimede [15] che perviene piuttosto tardi all’attenzione degli intellettuali europei. Come ricordato da Clagett [16, 17], la prima traduzione in latino di quest’opera (a partire dal “manoscritto A”) venne effettuata solo nel 1450 da Giacomo da Cremona; l’evento cruciale che ne garantì la diffusione fu la sua inclusione nell’editio princeps dell’opera di Archimede, che venne stampata a Basilea nel 1544. Molto probabilmente, Magnenus ne viene a conoscenza per tramite del commento di Clavio al libro Sulla sfera del cosmo di Giovanni Sacrobosco (1581), che include una Digressio de arenae numero , che si rifà direttamente a L’Arenario. Rimandiamo a [7] per una discussione più completa a proposito.

2. Il primo tentativo di contare gli atomi

Magnenus osserva che l’odore di un piccolo grano d’incenso si distribuisce in una intera stanza e, da qui, stima che esso può essere suddiviso in un miliardo di porzioni circa, ognuna delle quali (in ottemperanza all’idea dell’atomismo) contiene degli atomi di sostanza odorosa. A questo punto c’è il passaggio delicato e cruciale: come stimare il numero di atomi in ognuna di quelle porzioni? È chiaro che non c’è modo di usare la vista; parti con dimensioni di pochi millesimi di millimetro sono di per sé invisibili.

Magnenus inizia il ragionamento appoggiandosi ad una considerazione naturalistica. Ponderando attentamente le particolarità di un piccolo insetto, come una zanzara, in prospettiva atomistica, si convince che, affinché esso possa manifestare una tale “indescrivibile perfezione”, deve includere tante parti e dunque tantissimi atomi. Si noti che lo spunto viene da un brano di Plinio, ma l’interpretazione proposta da Magnenus è in linea con il pensiero di Democrito.

Per procedere oltre e ottenere una stima quantitativa, Magnenus si ispira ad Archimede nel modo che segue. Il grande siracusano, sulla base del modello eliocentrico di Aristarco, s’era chiesto perché le stelle non sembrano spostarsi durante l’anno, quando la terra gira intorno al sole. Aveva concluso che tutte le stelle, anche le più vicine, dovessero essere abbastanza lontane da noi da sembrare in pratica fisse. Per formulare una proposta definita, ne L’Arenario [15] egli ipotizza la seguente proporzione:

raggio della Terra : distanza Terra-Sole = distanza Terra-Sole : distanza delle stelle

Magnenus fa esplicito richiamo ad Archimede e decide di regolarsi nello stesso modo, supponendo che l’estensione del grano di incenso e di ciascuna delle porzioni - o se si vuole, la sostanza in essi contenuta - siano nella seguente proporzione:

grano di incenso : porzione di incenso = porzione di incenso : atomo di incenso

Siccome il primo termine corrisponde al numero delle porzioni, e vale circa un miliardo, il numero di atomi, dato approssimativamente dal rapporto tra l’estensione dell’intero grano e quella di un singolo atomo, vale circa un miliardo di miliardi.

Per la cronaca, tanto la distanza delle stelle più vicine quanto le dimensioni (e il numero) degli atomi verranno determinate per la prima volta solo due secoli dopo Magnenus. Nel 1838, Bessel osserverà uno spostamento apparente di 0,314 secondi d’arco della stella 61 Cygni [18]. Nel 1865, Loschmidt stimerà in un milionesimo di millimetro la grandezza delle molecole di aria [19].

Sottolineiamo che il linguaggio delle proporzioni, con cui oggi ci familiarizziamo sin dalla seconda media, aiuta a presentare la congettura a un lettore moderno, ma non è quello che viene usato nel testo di Magnenus che, come è facile immaginare, è un po’ involuto da leggere e difficile da apprezzare (vedi [7] per una traduzione). I calcoli numerici nel testo originale sono i seguenti:

si osserva che l’incenso contenuto in un grano grande come un pisello, dopo la combustione, può essere percepito in una stanza che, misurata in unità del grano stesso, ha lati pari a 720, 900 e 1.200 grani, ovvero con un volume circa un miliardo di volte quello del grano;
si congettura che ognuna delle porzioni di gas, in cui la stanza rimane suddivisa, contenga tanti “atomi di elemento” quante sono le parti della stanza, ovvero, un miliardo circa.

La congettura si rifà a uno dei principi base del pensiero del Rinascimento, la corrispondenza tra macrocosmo e microcosmo; mentre questo può causare a un moderno lettore un’impressione di straniamento, va riconosciuto che, nella forma, l’argomentazione combacia con quella di Archimede. La figura 2 riassume le due congetture e ne evidenzia il forte parallelismo.

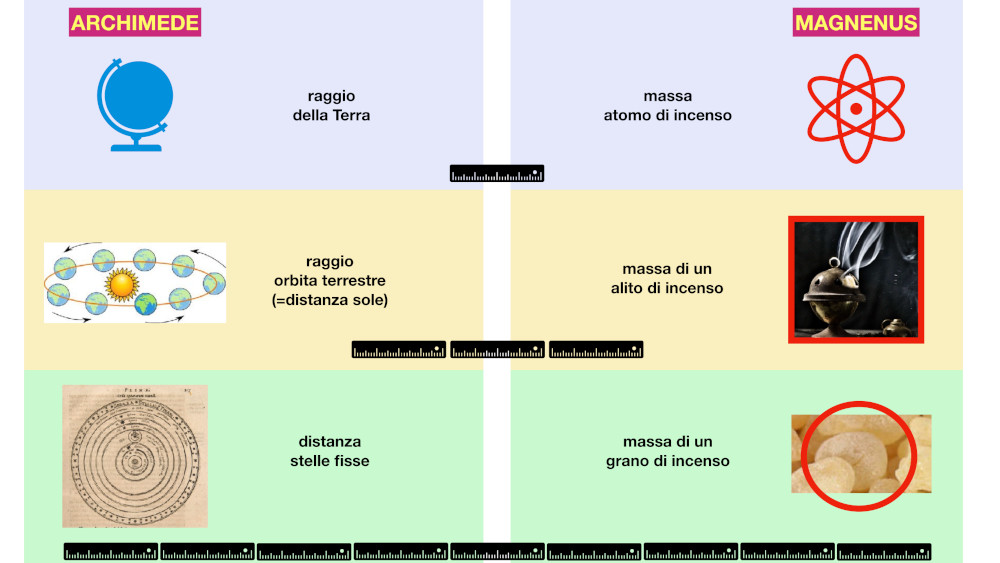
Vissani.pdf

Figura 2 . Confronto tra la congettura sulla distanza delle stelle fisse (di Archimede, a sinistra) e quella sul numero di “atomi” presenti in un grano di incenso (di Magnenus, a destra); nel secondo caso, per agevolare un lettore moderno utilizziamo il concetto di massa, anche se il testo originario si riferisce all’estensione dei corpi solidi di interesse - grano, alito e atomo di incenso - ovvero, al loro volume: la differenza in pratica è piccola

3. Confronto con due moderne determinazioni

Compariamo adesso il numero di atomi esibiti da Magnenus con due stime moderne. La prima, diretta, è resa possibile dalla conoscenza che oggi abbiamo dell’atomo e delle molecole. La seconda ha il pregio di non presumere questa conoscenza e, per questo, è più vicina in spirito all’approccio del Democrito redivivo ; essa, invece di usare la proporzione congetturata da Magnenus, si basa un modello semplificato di come funziona il nostro sistema olfattivo. Discuteremo la differenza tra i due risultati e mostreremo che il valore stimato da Magnenus si piazza tra questi due.

3.1 Una stima moderna del numero di molecole

La prima stima si basa sulla conoscenza (moderna) di quanto pesano le singole molecole. Immaginiamo che il grano di incenso sia una sferetta di raggio r , per cui il suo volume è:

v = \frac{4 π}{3} r^{3}

Siccome la densità dell’incenso, ρ, è pari a 1,06 g/cm³, se il raggio, r, del grano è uguale 5 mm, la massa della sferetta vale ρ × v = 0,55 g. Secondo l’atomismo, questa massa corrisponde al prodotto del numero delle molecole per la loro massa. Supponiamo, allora, che il grano sia costituito da molecole di massa atomica 456 u.m.a. - come l’acido boswellico, che conferisce odore all’incenso [20]. Dividendo la massa della sferetta per quella della molecola, stimiamo che essa contiene settecento miliardi di miliardi di molecole - ovvero 7 × 10²⁰ , da confrontare con il valore esibito da Magnenus: N = 7,776 × 10¹⁷ ; entro un fattore 1000 ci siamo. È questo l’accordo che ha colpito molti commentatori moderni.

Vediamo ora cosa si può dire sulle dimensioni delle molecole, che per semplicità assumiamo sferiche e di raggio a . Il volume v del grano, al netto di un fattore f che tiene conto del vuoto tra le molecole, può essere eguagliato al numero di molecole per il volume di ognuna di esse:

f \times v = N \times \frac{4 π}{3} a^{3}

Dunque, abbiamo $a = r \times \sqrt[3]{f / N}$ . Il valore preciso di f non è davvero essenziale; se consideriamo f = 0,74, che è quello corrispondente all’impacchettamento ottimale [21], assieme al valore di N congetturato da Magnenus, troviamo:

a = 5 milionesimi di mm

Questo valore è appena 5 volte più grande delle dimensioni stimate da Loschmidt. Se lo confrontassimo con il raggio di Bohr, aumentato della radice cubica di 456 per tenere rozzamente conto del numero degli atomi, troveremmo un valore una decina di volte più piccolo di a ; di nuovo, un accordo discreto (confrontare con le conclusioni riportate in [3]).

Vissani-Figura 3.pdf

Figura 3 . Rappresentazione schematica di uno strato di molecole di aria (in celeste) e di alcune particelle di sostanze odorose (in rosso) a contatto con la superficie sensibile del naso; il volume sensibile è dato dal prodotto della superficie sensibile A _sens e del diametro delle particelle di sostanza odorosa pari a 2a

3.2 Quanto son grandi le particelle odorose?

Ora confrontiamoci con una stima diversa, tanto per la procedura quanto per il valore delle dimensioni delle particelle a cui si perviene. Invece di seguire il metodo delle proporzioni, descritto sopra, ci basiamo su un semplice modello del senso dell’odorato. Anche questa stima è coerente con i principi dell’atomismo; ci riferiamo all’idea, attribuita da Aristotele a Democrito (per criticarlo), che ogni senso sia una forma del tatto [22]: “Democrito e la maggior parte dei filosofi della natura che trattano della percezione sensoriale [...] rappresentano tutti gli oggetti del senso come oggetti del tatto. [...] ne consegue che ciascuno degli altri sensi è un modo del tatto.” Assumeremo allora che un odore possa essere percepito a patto che sulla superficie sensibile del naso cada un certo numero di particelle odorose N _sens ≥1.

La densità di particelle nella stanza dove si diffondono i fumi dell’incenso vale semplicemente N/V ; seguendo Magnenus, il volume V della stanza può essere messo in relazione al volume di ogni grano di incenso v come segue:

V = 1,5 × 10⁹ × v

Infatti, ricordiamo che le tre dimensioni lineari della stanza sono date da Magnenus in unità del grano di incenso e, perché questa misura abbia senso, bisogna ipotizzare che il grano abbia forma approssimativamente sferica, come già supposto; pertanto, il volume della stanza è:

V = 720 × 900 × 1200 × (2 r )³

dove v = 4π/3 × r³ . La densità N/V va eguagliata a quella a contatto con la superficie olfattiva; assumendo che tale superficie abbia area pari a A _sens , abbiamo l’equazione:

\frac{N_{sens}}{2 a A_{sens}} = \frac{N}{V}

Nell’equazione a indica il raggio della particella odorosa (assunta sferica), mentre il denominatore della prima frazione rappresenta il volume di un parallelepipedo con una altezza pari al diametro 2a di tale particella (Figura 3).

A questo punto disponiamo di due espressioni per il numero di particelle:

N = \frac{3 f}{4 π a^{3}} v

N = \frac{N_{sens}}{2 a A_{sens}} V

Confrontandole, troviamo che le dimensioni lineari a delle particelle odorose nel fumo d’incenso valgono:

a = \sqrt{\frac{3 f}{2 π} \times \frac{v}{V} \times \frac{A_{sens}}{N_{sens}}}

Tale formula non dipende direttamente dai due volumi v e V , ma solo dal loro rapporto. Utilizzando i valori sopra discussi di v/V e f con l’ipotesi che A_sens ≈ 10 cm² , concludiamo che:

a = \frac{0,5 μm}{\sqrt{N_{sens}}}

Dunque, il valore massimo è una frazione di micron. Nel caso che N_sens non sia troppo lontano dall’unità, si tratta delle tipiche dimensioni di una particella di particolato ultra-fine, di grandezza simile a quelle delle particelle di fumo che provengono dalla combustione dell’incenso, come risulta da moderne determinazioni quantitative [23]. Per esempio, se N _sens = 1 (oppure 100) abbiamo un valore 100 (oppure 10) volte più grande del precedente; ovviamente, le dimensioni del particolato sono maggiori di quelle delle singole molecole.

3.3 Osservazioni

Per concludere il confronto, ci basterà riportare le stime approssimate del numero di parti minime (‘atomi’) contenute nel grano di incenso assieme al valore esibito da Magnenus:

\begin{matrix} stima & procedura \\ 10^{21} & conteggio del numero di molecole \\ 10^{18} & proporzione postulata da Magnenus \\ 10^{16} & particelle odorose assumendo N_{sens} = 100 \end{matrix}

Per ottenere l’ultima determinazione, abbiamo usato l’espressione di a data subito sopra assieme alla formula $a = r \times \sqrt[3]{f / N}$ . Come mostrato da questa tabella, il valore congetturato da Magnenus si situa giusto tra le due determinazioni appena discusse.

Annotazioni

Per prima cosa ci sembra importante sottolineare che la congettura di Magnenus sul numero di atomi (la prima, da quanto ne sappiamo!) non può essere considerata una determinazione quantitativa; è semplicemente una congettura; in effetti, il termine con cui il suo autore la indica è proprio quello di conjectura . Si deve però osservare che, nelle discipline ipotetico-deduttive, la fase di formulazione delle ipotesi ha un’importanza cruciale, almeno sin dal tempo della scienza matematica ellenistica. E, se pure si riconosce l’azzardo (o audacia) che c’è dietro questo passo, non si dovrebbe ignorarne l’accordo con le determinazioni quantitative che sono possibili oggi, magari di carattere fortuito, ma comunque sempre sostanziale, o tanto meno disconoscerne il ruolo storico; si veda [7] per una rassegna delle posizioni di storici e filosofi a proposito.

Parlare di queste cose a scuola può offrire spunti di qualche valore didattico; per esempio, può suggerire di: 1) applicare la geometria alla modellizzazione della realtà fisica; 2) discutere come funzionano i sensi; 3) accedere più direttamente alle idee di Archimede (vedi, ad es., [24]); 4) intraprendere percorsi interdisciplinari con i docenti di filosofia, storia e/o latino, alcuni dei quali son stati già sperimentati con un certo successo [25]; 5) confrontarsi con questioni di metodo scientifico e di storia della scienza; ecc. Non sembra irragionevole ritenere che approcci del genere potrebbero rendere più stimolante e agevole l’accesso all’idea moderna di atomo.

Ringraziamenti

Son grato al programma PRIN 2017 del MIUR che finanzia il progetto NAT-NET: Neutrino and Astroparticle Theory Network, no. 2017W4HA7S e, soprattutto, a Marco Ciardi, Antonio Clericuzio, Silvano Fuso, Paolo Mazzarello, Paolo Venti e ai due revisori anonimi di CnS i per preziosi commenti.

Riferimenti

[1] Chrysostomi Magneni, Democritus reviviscens, sive, DE ATOMIS. Apud Andream Magrium, Papiæ (Pavia), 1646.

[2] J. N. Murrell, Avogadro and His Constant , Helvetica Chimica Acta , 2001, 84 , 1314.

[3] K. Ruedenberg, W. H. E. Schwarz, Three Millennia of Atoms and Molecules , Pioneers of Quantum Chemistry , capitolo 1, 2013.

[4] M. Quack, The Concept of Law and Models in Chemistry , European Review , 2014, 22 , No. S1, 50.

[5] E. Massa, G. Mana, Counting atoms, Nature Physics , 2016, 12 , 522.

[6] M. Malvaldi, L’infinito tra parentesi. Storia sentimentale della scienza da Omero a Borges, Rizzoli, 2017.

[7] F. Vissani, Il primo tentativo documentato di contare gli atomi, Quaderni di cultura scientifica , 2022, 9 DOI: 10.13140/RG.2.2.35683.02081).

[8] P. Mazzarello G. Mellerio, Jean-Chrysostome Magnen , 2013, in Almum studium Papiense . Storia dell’Università di Pavia, 1/II, a cura di D. Mantovani, Cisalpino-Monduzzi, Milano, 2013.

[9] Scheda su Magnenus in The Galileo Project compilata da R. S. Westfall ( http://Galileo.rice.edu/ Catalog/NewFiles/Magnenus.html ).

[10] A. G. M. Van Melsen, Da atomos a atomo: storia del concetto di atomo (tradotto dall’olandese del 1949), Società editrice internazionale, Torino, 1957.

[11] A. Clericuzio, Elements, Principles and Corpuscles. A Study of Atomism and Chemistry in the Seventeenth Century, Kluwer Academic Publisher, 2000 (parte di: International Archives of the History of Ideas).

[12] L. L. Whyte, Essay on Atomism, from Democritus to 1960, Middletown, Connecticut, Wesleyan University Press, 1961.

[13] W. Charleton, PHYSIOLOGIA Epicuro-Gassendo-Charltoniana: or a fabrick of science natural, upon the hypothesis ATOMS - Founded by Epicvrvs, repaired by Petrvs Gassendvs, augmented by Walter Charleton, Printed by Tho. Newcomb, London, 1654.

[14] R. S. Westfall, Unpublished Boyle papers relating to scientific method – II, Annals of Science , 1956, 12 , 103.

[15] Archimede (c. 287 - 212 a C), L’Arenario, traduzione di H. F. Fleck, Quaderni di Scienze Umane e Filosofia Naturale, 2016, 2 , 1 ( http://www.heinrichFleck.net/quaderni/Arenarius.pdf )

[16] M. Clagett, Archimedes , Dictionary of Scientific Biography I, 1970, 228-229.

[17] Per un breve e utile estratto, si veda https://www.historyofinformation.com/detail.php?id=2864

[18] F. Bessel, Bestimmung der Entfernung des 61sten Sterns des Schwans , Astronomische Nachrichten , 1839, 16 , 65.

[19] J. Loschmidt, On the Size of the Air Molecules , Proceedings of the Academy of Science of Vienna , 1865, 52 , 395 (traduzione in https://loschmidt.chemi.muni.cz/biography/pdf/discovery.pdf)

[20] E. Ernst, Frankincense: systematic review , British Medical Journal , 2008, 337 , a2813.

[21] Si veda, per esempio, Wikipedia sulla “Congettura di Keplero” e sulla sua storia (https://it.wikipedia.org/wiki/Congettura_di_Keplero)

[22] Aristotele (384 - 322 a C), De sensu (traduzione di J.A. Smith, W.D. Ross, The Works of Aristotles, Oxford, 1907 ( https://digitalassets.lib.berkeley.edu/main/b20762564_C005621977.pdf )

[23] Y. S. Cheng, W. E. Bechtold, C. C. Yu, I. F. Hung, Incense Smoke: Characterization and Dynamics in Indoor Environments, Aerosol Science and Technology , 1995, 23 (3), 271.

[24] L. Russo, Archimede. Un grande scienziato antico, Carocci, 2019.

[25] Un breve resoconto giornalistico dell’esperienza didattica su Magnenus condotta a Pordenone nell’anno scolastico 2016-2017 grazie all’iniziativa del professor Paolo Venti: https://www.ilgazzettino.it/pay/nazionale_pay/certamen_32_latinisti_a_caccia_di_un_premio- 2358666.html .