Abstract. Usually, at the level of basic chemistry in the first two years of secondary school, the reaction rate is defined by referring to the average speed; sometimes and only briefly the concept of instantaneous speed is mentioned.
In this article a possible in-depth analysis of the instantaneous reaction rate is provided; the analysis is not based on a theoretical-descriptive way, but uses an experimental-inductive approach.
Keywords: velocità di reazione; velocità istantanea; velocità media; coefficiente angolare di una retta
È noto che, anche a livello di chimica di base, la velocità di reazione si definisce con riferimento alla variazione della quantità di sostanza di un determinato componente della reazione nel corso del tempo.
Però, dato che la velocità con la quale cui si consumano i reagenti e si formano i prodotti cambia durante la reazione, è necessario considerare la velocità di reazione istantanea, ossia la velocità in un determinato istante.
Quindi, a rigore, essa è definita formalmente come la variazione infinitesima della quantità di un componente (reagente o prodotto) di una reazione in un intervallo di tempo infinitamente piccolo, cioè in un intervallo di tempo infinitesimo. Essa corrisponde al coefficiente angolare (a prescindere che sia positivo o negativo) della tangente in un determinato punto alla curva che riporta come varia la quantità di un reagente o prodotto in funzione del tempo [1]-[3].
Data la definizione di velocità di una reazione come rapporto tra la variazione della quantità di reagente o prodotto, ∆m, e il relativo intervallo di tempo, ∆t:
velocità = ∆m/∆t
la velocità istantanea si ottiene quando ∆t diventa infinitamente piccolo:
velocità istantanea = ∆m/∆t (con ∆t → 0)
Così, per l’insegnamento della chimica di base, in un testo molto datato [4] era descritta in dettaglio anche la misura della velocità istantanea di reazione, sfruttando il calcolo del coefficiente angolare che era insegnato (come tuttora) nel corso di matematica del primo biennio della “scuola media superiore”.
In questo modo, diversi anni fa, la definizione di velocità istantanea era introdotta abbastanza rigorosamente sebbene rimanesse da spiegare, da parte dell’insegnante di chimica, la corrispondenza del coefficiente angolare della tangente alla curva con la velocità istantanea.
Attualmente, invece, per quanto riguarda la velocità di reazione ci si limita a dire solo che essa è uguale al rapporto fra la variazione della quantità di materia consumata o prodotta e l’intervallo di tempo richiesto per tale variazione, parlando semplicemente di:
- velocità media se l’intervallo di tempo è ampio
- velocità istantanea se l’intervallo di tempo è brevissimo
Ciò forse è dovuto al fatto di ritenere un approfondimento della velocità istantanea di trascurabile importanza culturale o troppo impegnativo a livello del secondo anno del primo biennio della scuola secondaria di secondo grado.
Al contrario, per la nostra esperienza, tale approfondimento, al pari di altre definizioni e concetti scientifici:
- presuppone una trattazione in chiave multidisciplinare adeguata per “sviluppare il territorio dell’interdisciplinarità, della mutidimensionalità, del reale e della complementarietà dei saperi” del nuovo paradigma della complessità, come auspicato anni fa in CnS [5]-[6];
- consente una definizione di velocità istantanea senza il ricorso ai concetti di trigonometria, limite e derivata;
- interessa molti ragazzi animati da particolare motivazione per le discipline scientifiche;
- non richiede grande dispendio di tempo ed è alla portata delle capacità di apprendimento degli studenti del secondo anno del primo biennio.
A tale scopo viene proposto un possibile approccio induttivo-sperimentale, utilizzando la reazione fra marmo (CaCO3) e acido cloridrico, che viene di solito effettuata, assieme ad altri esperimenti di cinetica, per evidenziare l’influenza della superficie di contatto dei reagenti sulla velocità di reazione.
Tale esperimento consiste nel misurare la diminuzione di massa di una stessa quantità di marmo in uno stesso intervallo di tempo, variando la granulosità del marmo, ma utilizzando le medesime modalità sperimentali. Nel caso specifico ci si è concentrati solo sulla misura della velocità di reazioni usando una sola granulosità del marmo.
2. Descrizione dell’esperimento per l’approfondimento della velocità istantanea di reazione
La reazione in questione è:
CaCO3(s) + 2HCl(aq) → CaCl2(aq) + CO2(g) + H2O(l) (I)
che produce diossido di carbonio con conseguente diminuzione di massa di reazione, cosa che è evidenziata da ragazzi tramite la bilancia di adeguata precisione.
Però, in questo caso, non si misura la diminuzione di massa in un certo intervallo di tempo, ma la progressiva diminuzione di massa (minuto dopo minuto) fino a quando non si osserva più nessuna variazione (termine della reazione).
2.1 Obiettivi
Guidare gli allievi, mediante una discussione interattiva dei risultati sperimentali ottenuti e sfruttando le loro conoscenze e abilità in matematica e fisica, alla comprensione del motivo per cui la velocità istantanea corrisponde al coefficiente angolare della tangente in uno specifico punto alla curva che riporta la variazione della quantità di sostanza in funzione del tempo.
2.2 Reattivi e strumenti
- becker da 250 mL
- vetrini da orologio
- pezzetti di marmo con massa compresa fra 1-2 g
- soluzione di acido cloridrico 6 M
- bilancia digitale o analogica a lettura immediata in grado di apprezzare la seconda cifra decimale
- orologio contasecondi (o cronometro)
2.3 Procedimento
Si versano circa 50 mL di soluzione di HCl nel becker e si pone sul piatto della bilancia. Si copre con un vetrino e si legge la massa. Si pongono sul vetrino i pezzetti di marmo la cui massa deve essere compresa fra 1 e 2 g.
Dopo avere annotato la massa di tutto il sistema, si introduce il marmo nel becker e si copre immediatamente con il vetrino per impedire la fuoriuscita di gocce di liquido.
La reazione produce gas CO2 che esce attraverso il beccuccio del becker.
Quindi, mediante l’orologio contasecondi, si registra ogni minuto la progressiva diminuzione di massa a partire dal momento in cui i reagenti vengono a contatto fino a quando non si osserva più alcuna variazione.
Con i dati ottenuti ogni gruppo di studenti costruisce il grafico relativo alla variazione della massa in funzione del tempo e calcola il coefficiente angolare relativo ad un dato istante prefissato dall’insegnante e diverso per ogni gruppo.
Così ogni gruppo di allievi può ottenere, senza problemi di sicurezza e in tempo breve, i dati sperimentali necessari per approfondire, in una fase successiva all’attività sperimentale, il concetto di velocità istantanea.
A titolo di esempio, si riportano in figura 1 i dati sperimentali e il grafico della variazione della massa di CaCO3 (s) in funzione del tempo, per la reazione (I), ottenuti diversi anni fa da un gruppo di allievi di una classe del primo biennio dell’IPSIA “G. Ceconi” di Udine.
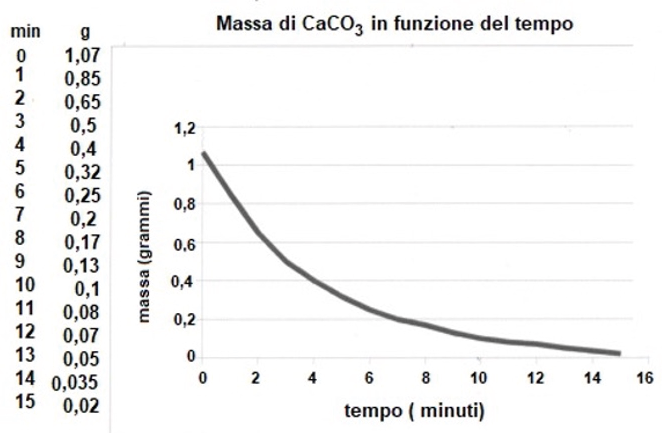
Figura 1. Grafico della massa di marmo in funzione del tempo (minuti)
A questo punto, si chiede agli studenti di calcolare i coefficienti angolari delle tangenti alla curva del grafico relativamente ad alcuni istanti assegnati.
Nella discussione relativa all’esperimento, i ragazzi vengono guidati alla “scoperta” del motivo per cui la velocità istantanea corrisponde al coefficiente angolare della tangente alla curva della variazione di massa rispetto al tempo, utilizzando i loro grafici e i calcoli dei coefficienti angolari.
A tale scopo, ad esempio, si invitano gli allievi a congiungere, come riportato in figura 2, il punto A con il B nella curva variazione di massa (grammi)/tempo (minuti), ottenendo la secante della curva.
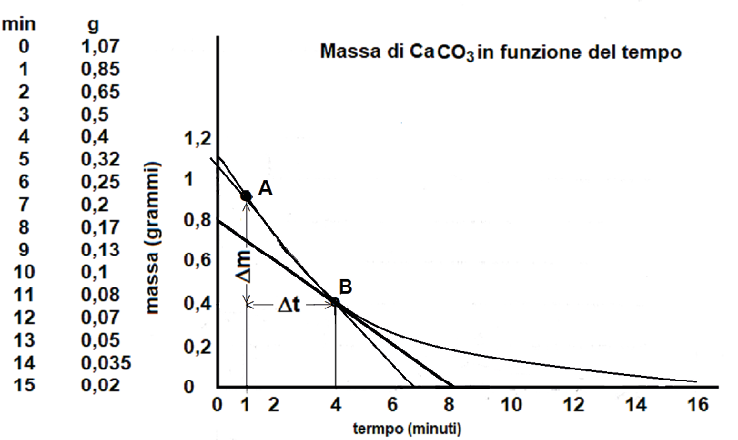
Figura 2. Grafico della secante e della tangente relativa all’istante t = 4 minuti
Quindi indicando con:
∆m = diminuzione di massa di CaCO3 in grammi fra i punti A e B (decremento ordinata)
∆t = intervallo di tempo in minuti fra i punti A e B (incremento ascissa)
si fa notare che il coefficiente angolare di tale retta secante, dato dal rapporto ∆m/∆t, corrisponde alla velocità media relativa al tempo ∆t impiegato per la trasformazione di ∆m grammi di marmo:
velocità media = ∆m (g)/∆t (min)
Pertanto, utilizzando la figura 2, gli studenti comprendono abbastanza facilmente che, quando ∆t diventa piccolissimo, il punto A si approssima al punto B e, quanto più A si avvicina a B, tanto più la retta secante si avvicina alla tangente alla curva nel punto B.
In particolare, riferendosi ai coefficienti angolari della retta secante e della tangente, risulta evidente il motivo per cui la velocità istantanea corrisponde al coefficiente angolare della tangente alla curva variazione di massa/tempo nell’istante in esame.
Come ultima considerazione si può aggiungere che la velocità istantanea altro non è che velocità media considerando un intervallo di tempo tendente a zero.
L’approfondimento proposto in questo articolo richiede un tempo supplementare rispetto a quello normalmente dedicato alla trattazione della cinetica nel primo biennio della scuola secondaria di secondo grado, ma suscita molto interesse e curiosità negli studenti più impegnati nello studio.
Inoltre, si ritiene che esso non sia di trascurabile significato culturale perché, come si è detto, anzitutto permette all’insegnante di introdurre la complessità disciplinare senza rinunciare a una definizione abbastanza rigorosa e approfondita, senza far ricorso ai concetti di trigonometria, limite e derivata.
Consente, inoltre, agli allievi di “trovare” una spiegazione non mnemonica della velocità istantanea, applicando utilmente le loro conoscenze e abilità a livello del primo biennio.
Se l’insegnante lo ritiene adeguato alle capacità d’apprendimento dei suoi allievi, la discussione può iniziare partendo da una retta secante congiungente due punti, uno antecedente e un altro successivo a quello relativo all’istante considerato.
Infatti, nel linguaggio matematico, la velocità all’istante t è definita come il limite della velocità media in un intervallo ∆t avente t come estremo, oppure comprendente t, quando l’ampiezza dell’intervallo tende a zero. In ogni caso, al tendere di ∆t a zero, la retta secante si approssima sempre più alla posizione della tangente e il suo coefficiente angolare tende a diventare uguale a quello della tangente.
In tale modo, si spiega la “corrispondenza” della velocità istantanea con il coefficiente angolare della tangente alla curva variazione di massa/tempo.
Questo vale anche nel caso particolare in cui la retta secante sia parallela a quella tangente. Solo che, in questo caso, come si può notare dalla figura 3, la velocità all’istante t = 4 min è uguale alla velocità media corrispondente all’intervallo di tempo ∆t = 8 min, cioè il coefficiente angolare della retta secante parallela è uguale a quello della retta tangente, perché le due rette sono parallele.
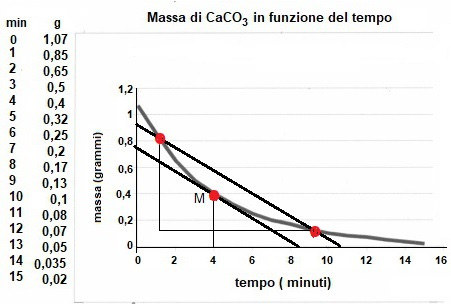
Figura 3. Caso particolare della retta secante parallela alla tangente
Riferimenti
[1] P. W. Atkins, J. De Paula, Elementi di chimica fisica, Zanichelli Editore, Bologna, 2018.
[2] P. W. Atkins, J. De Paula, J. Keeler, Chimica Fisica, Zanichelli Editore, Bologna, 2020.
[3] C. Vallance, An Introduction to Chemical Kinetics, Morgan and Claypool Publishers, San Rafael, California, 2017.
[4] M. Lewis, G. Waller, La chimica: fatti e idee, Zanichelli Editore, Bologna 1988.
[5] G. Villani, La chimica nella Scuola - CnS, 2009, 2, 109.
[6] P. Ambrogi, M. A. Floriano, E. Ghibaudi, La chimica nella Scuola - CnS, 2005, 1, 9.